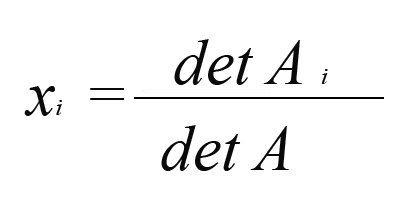Инструкция
1
Запишите заданную систему уравнений. Составьте ее матрицу. При этом первый коэффициент первого уравнения соответствует начальному элементу первой строки матрицы. Коэффициенты из второго уравнения составляют вторую строку матрицы. Свободные члены записываются в отдельный столбец. Заполните таким образом все строки и столбцы матрицы.

2
Вычислите главный определитель матрицы. Для этого найдите произведения элементов, расположенных по диагоналям матрицы. Сначала умножьте все элементы первой диагонали, расположенной от левого верхнего до нижнего правого элемента матрицы. Потом вычислите так же вторую диагональ. От первого произведения отнимите второе. Результат вычитания и будет главным определителем системы. Если главный детерминант не равен нулю, значит система имеет решение.
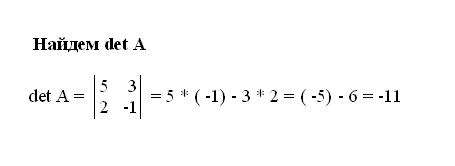
3
Затем найдите вспомогательные определители матрицы. Сначала вычислите первый вспомогательный определитель. Для этого замените первый столбец матрицы столбцом свободных членов решаемой системы уравнения. После этого определите детерминант полученной матрицы по аналогичному алгоритму, как описано выше.
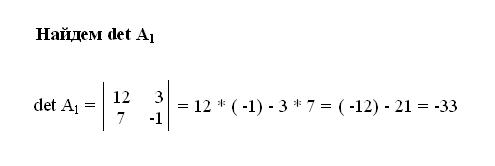
4
Подставьте вместо элементов второго столбца исходной матрицы свободные члены. Вычислите второй вспомогательный определитель. Всего количество данных детерминантов должно быть равно числу неизвестных переменных в системе уравнений. Если все полученные детерминанты системы равны нулю, считается, что система имеет множество неопределяемых решений. Если нулю равен лишь главный определитель – система несовместима и корней у нее нет.
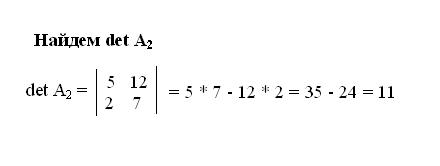
5
Найдите решение системы линейных уравнений. Первый корень вычисляется, как частное от деления первого вспомогательного определителя на главный детерминант. Запишите выражение и посчитайте его результат. Второе решение системы вычислите так же, поделив второй вспомогательный определитель на главный детерминант. Запишите полученные результаты.
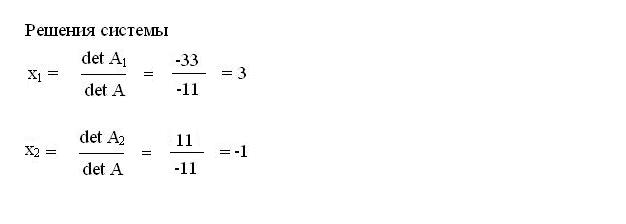
Видео по теме