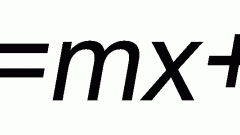Инструкция
1
Запомните, что основой или базой для решения любых уравнений являются тождественные преобразования. Они позволяют решать все виды уравнений: и тригонометрические, и показательные, и иррациональные. Учтите, что существует два вида тождественных преобразований. Первый заключается в том, что к обеим частям уравнения вы можете прибавить или отнять одно и то же число или выражение (любое, в том числе и с неизвестной величиной). Второй вариант тождественных преобразований: обе части уравнения вы вправе умножить (разделить) на одно и то же выражение или одно и то же число (кроме ноля). Посмотрите, как это работает на примере линейного уравнения ((х+2)/3)+х=1-3/4х
2
Чтобы сократился знаменатель, умножьте обе части дроби на 12. То есть приведите ее к общему знаменателю. Тогда сократится и тройка, и четверка. Получите следующее выражение: (x+2)/3+х=1-3/4х.
3
Раскройте скобки, получив выражение вида: 12((х+2)/3+х)=12(1-3/4х)
4
Сократите дробь: 4(х+2)+12х=12-9х
5
Раскройте скобки: 4х+8+12х=12-9х
6
7
Учтите, что алгебра популярна квадратными уравнениями. Запомните практические приемы, которые позволят вам из-за невнимательности снизить количество ошибок при решении квадратных уравнений. Не ленитесь, любое квадратное уравнение приводите к линейному виду, правильно выстраивайте свой пример. Впереди икс в квадрате, потом простой икс, последним свободный член. Далее постарайтесь избавляться от отрицательного коэффициента, для его ликвидации умножайте части уравнения на -1. При наличии в уравнении дробных коэффициентов стремитесь избавиться от дробей, умножением всего уравнения на соответствующий множитель. Проверяйте корни по теореме Виета.
Видео по теме