Инструкция
1
Понятие нормы универсально для любой матрицы, квадратной или неквадратной, матрицы-столбца или строки, размерность также может быть любой. Эта характеристику используют в качестве оценочной величины для анализа изменяемости матрицы в каком-либо расчетном процессе или совокупности нескольких матриц.
2
Можно сказать, что норма является показателем «мощности» матрицы. Она обозначается ‖A‖ и равна действительному числу, которое должно соответствовать определенному набору условий:‖А‖ ≥ 0, причем равенство нулю выполняется только для нулевой матрицы;‖а•А‖ = ‖а‖•‖А‖, где а принадлежит множеству рациональных чисел;‖А+В‖ ≤ ‖А‖ + ‖В‖ - коммутативность.
3
Норма, для которой выполняется также свойство ‖А•В‖ ≤ ‖А‖ • ‖В‖, называется мультипликативной. Существует три вида норм: бесконечная, первая и евклидова. Все они являются каноническими, т.е. их значения не меньше по модулю любого матричного элемента. На практике обычно вычисляют только один из видов, этого достаточно для объективной оценки.
4
Чтобы найти норму матрицы, нужно воспользоваться одним из ниже приведенных способов для каждого вида. Все они основаны на расчете суммы элементов матрицы, но каждый подразумевает собственный алгоритм.
5
Для расчета бесконечной нормы просуммируйте по модулю значения элементов отдельно по каждой строке и выберите из них максимальное:‖A‖_1 = mах_i Σ_j |а_ij|.
6
Найдите первую норму, поступив аналогично с элементами по каждому столбцу:‖A‖_2 = mах_j Σ_i |а_ij|.
7
Расчет евклидовой нормы подразумевает три действия: возведение каждого элемента в квадрат, суммирование и извлечение квадратной корня из общего результата:‖A‖_3 = √Σа²_ij.
8
Пример: вычислите все виды норм для данной матрицы.
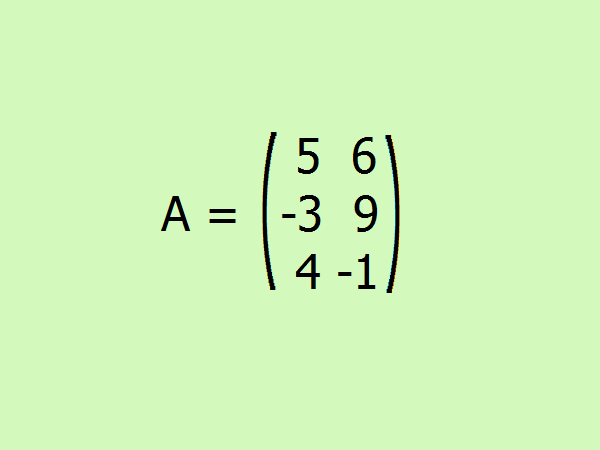
9
Решениеa11+a12=11; a21+a22=12; a31+a32=5 → ‖А‖_1 = 12;a11+a21+a31=12; a12+a22+32=16 → ‖А‖_2 = 16;‖А‖_3 = √(25+36+9+81+16+1) = √168 ≈ 13.