Медиана - это отрезок, проведенный из некоторого угла многоугольника к одной из его сторон таким образом, что точка пересечения медианы и стороны является серединой этой стороны.
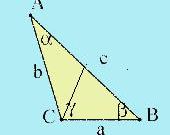
Пусть задан треугольник ABC, надо построить медиану, падающую из угла C на сторону AB. По сути, задача сводится к разбиению стороны AB пополам с помощью циркуля. Отдельно будет рассмотрено разбиение этого отрезка пополам, а потом будет представлена общаякартина.
2
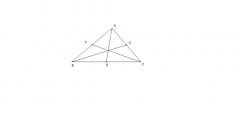
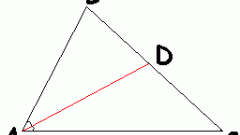
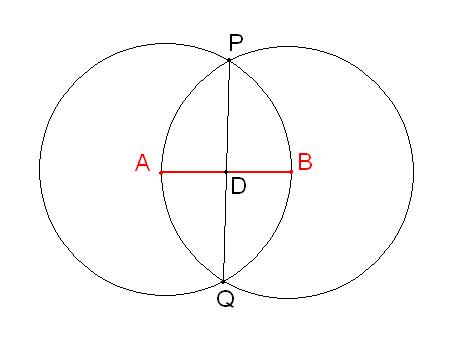
Сначала установите иглу циркуля в точку A, растворите циркуль так, чтобы он доставал грифелем до точки B. Проведите циркулем окружность с центром в точке A радиусом AB. Затем установите иглу циркуля в точку B и проведите такую же окружность с центром в точке B. Эти окружности пересекаются в двух точках, которые на рисунке обозначены как P и Q. Соедините точки P и Q по линейке. Точка пересечения отрезков PQ и AB будет серединой отрезка AB. Обозначьте ее D.
3
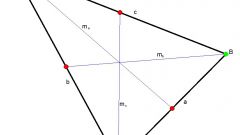
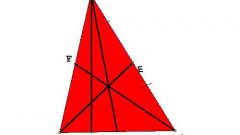
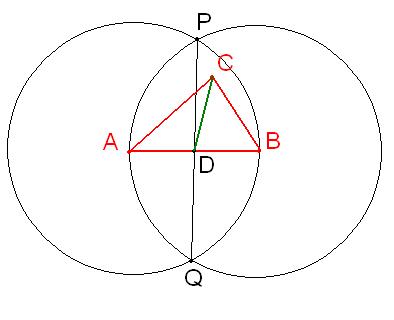
На рисунке изображена общая картина построений вокруг треугольника ABC. Теперь соедините найденную середину отрезка D с вершиной треугольника C. Отрезок CD является медианой треугольника.
