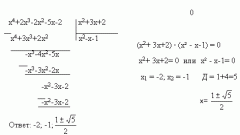Уравнение, представляющее собой квадратный трехчлен, обыкновенно называется квадратным уравнением. С точки зрения алгебры оно описывается формулой a*x^2+b*x+c=0. В данной формуле х - это неизвестное, которое требуется найти (его называют свободной переменной); a, b и c - числовые коэффициенты. В отношении компонентов указанной формулы существует ряд ограничений: так, коэффициент а не должен быть равен 0.
Значение неизвестного х, при котором квадратное уравнение превратится в верное равенство, называют корнем такого уравнения. Для того чтобы решить квадратное уравнение, необходимо сначала найти значение специального коэффициента - дискриминанта, который покажет количество корней у рассматриваемого равенства. Дискриминант вычисляется по формуле D=b^2-4ac. При этом результат вычисления может оказаться положительным, отрицательным или равным нулю.
При этом следует иметь в виду, что понятие квадратного уравнения требует, чтобы лишь коэффициент а был строго отличающимся от 0. Следовательно, коэффициент b может быть равным 0, а само уравнение в этом случае пример вид a*x^2+c=0. В такой ситуации следует использовать значение коэффициента, равное 0, и в формулах расчета дискриминанта и корней. Так, дискриминант в этом случае будет рассчитываться как D=-4ac.
В случае, если дискриминант квадратного уравнения оказался положительным, из этого можно сделать вывод, что данное равенство имеет два корня. Указанные корни можно вычислить по следующей формуле: x=(-b±√(b^2-4ac))/2a=(-b±√D)/2a. Таким образом, для расчета значения корней квадратного уравнения при положительном значении дискриминанта используются известные значения коэффициентов, имеющихся в уравнении. Благодаря использованию суммы и разности в формуле расчета корней результатом вычислений будут два значения, обращающие рассматриваемое равенство в верное.
В случае, если дискриминант квадратного уравнения оказался равным 0, можно сделать вывод о том, что указанное уравнение имеет один корень. Строго говоря, в этой ситуации корней у уравнения по-прежнему два, однако вследствие нулевого дискриминанта они будут равны между собой. В этом случае x=-b/2a. Если же в процессе вычислений значение дискриминанта оказывается отрицательным, следует сделать вывод о том, что рассматриваемое квадратное уравнение не имеет корней, то есть таких значений x, при которых оно обращается в верное равенство.
Решение уравнения: понятие дискриминанта
Значение неизвестного х, при котором квадратное уравнение превратится в верное равенство, называют корнем такого уравнения. Для того чтобы решить квадратное уравнение, необходимо сначала найти значение специального коэффициента - дискриминанта, который покажет количество корней у рассматриваемого равенства. Дискриминант вычисляется по формуле D=b^2-4ac. При этом результат вычисления может оказаться положительным, отрицательным или равным нулю.
При этом следует иметь в виду, что понятие квадратного уравнения требует, чтобы лишь коэффициент а был строго отличающимся от 0. Следовательно, коэффициент b может быть равным 0, а само уравнение в этом случае пример вид a*x^2+c=0. В такой ситуации следует использовать значение коэффициента, равное 0, и в формулах расчета дискриминанта и корней. Так, дискриминант в этом случае будет рассчитываться как D=-4ac.
Решение уравнения при положительном дискриминанте
В случае, если дискриминант квадратного уравнения оказался положительным, из этого можно сделать вывод, что данное равенство имеет два корня. Указанные корни можно вычислить по следующей формуле: x=(-b±√(b^2-4ac))/2a=(-b±√D)/2a. Таким образом, для расчета значения корней квадратного уравнения при положительном значении дискриминанта используются известные значения коэффициентов, имеющихся в уравнении. Благодаря использованию суммы и разности в формуле расчета корней результатом вычислений будут два значения, обращающие рассматриваемое равенство в верное.
Решение уравнения при нулевом и отрицательном дискриминанте
В случае, если дискриминант квадратного уравнения оказался равным 0, можно сделать вывод о том, что указанное уравнение имеет один корень. Строго говоря, в этой ситуации корней у уравнения по-прежнему два, однако вследствие нулевого дискриминанта они будут равны между собой. В этом случае x=-b/2a. Если же в процессе вычислений значение дискриминанта оказывается отрицательным, следует сделать вывод о том, что рассматриваемое квадратное уравнение не имеет корней, то есть таких значений x, при которых оно обращается в верное равенство.
