Вам понадобится
- Умение решать квадратные уравнения
Инструкция
1
Для того, чтобы решить квадратное неравенство методом интервалов, сперва нужно решить соответствующее квадратное уравнение. Переносим все члены уравнения с переменной и свободный член в левую часть, в правой части остается ноль. Корни квадратного уравнения, соответствующего неравенству (в нем знак "больше" или
"меньше" заменен на "равно") можно найти по известным формулам через дискриминант.
"меньше" заменен на "равно") можно найти по известным формулам через дискриминант.
2
На втором этапе мы записываем неравенство в виде произведения двух скобок (x-x1)(x-x2)<>0.
3
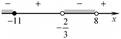
Отмечаем найденные корни на числовой оси. Далее мы смотрим на знак неравенства. Если неравенство строгое ("больше" и "меньше"), то точки, которыми отмечаем корни на координатной оси пустые, в противном случае ("больше или равно").
4
Берем число, левее первого (правого на числовой оси корня). Если при подстановке этого числа в неравенство, оно оказывается правильным, то интервал от "минус бесконечности" до самого малого корня является одним из решений уравнения, наравне с интервалом от второго корня до "плюс бесконечности". Иначе решением будет интервал между корнями.
Видео по теме
Обратите внимание
Не ошибитесь при решении соответствующего квадратного уравнения - в данном случае вы неправильно решите неравенство.
Полезный совет
Не забывайте о том, строгое или нестрогое неравенство решаете. Если неравенство строгое, то ставим круглые скобки (то есть не берем в интервал корень уравнения), иначе берем его в промежуток (ставим квадратные скобки).
Источники:
- Дорофеев Г. В. Учебник по алгебре для 7-ого класса
- как решить неравенство с корнем