Инструкция
1
Переходя к изучению неравенств с логарифмами, вы должны уже уметь решать логарифмические уравнения, знать свойства логарифмов, основное логарифмическое тождество.
2
Решение всех задач на логарифмы начинайте с нахождения ОДЗ - области допустимых значений. Выражение под логарифмом должно быть положительным, основание логарифма должно быть больше нуля и не равняться единице. Следите за равносильностью преобразований. ОДЗ на каждом шаге должно оставаться одним и тем же.
3
При решении логарифмических неравенств важно, чтобы с двух сторон от знака сравнения были логарифмы, причем с одним и тем же основанием. Если с какой-либо стороны представлено число, запишите его в виде логарифма, применяя основное логарифмическое тождество. Число b равняется числу a в степени log, где log - логарифм b по основанию a. Основное логарифмическое торжество является, по сути, определением логарифма.
4
Решая логарифмическое неравенство, обратите внимание на основание логарифма. Если оно больше единицы, то при избавлении от логарифмов, т.е. при переходе к простому числовому неравенству, знак неравенства остается тем же. Если основание логарифма от нуля до единицы, знак неравенства меняется на противоположный.
5
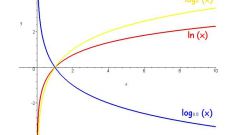
Полезно помнить ключевые свойства логарифмов. Логарифм единицы равен нулю, логарифм числа a по основанию a равен единице. Логарифм произведения равен сумме логарифмов, логарифм частного равен разности логарифмов. Если подлогарифменное выражение возводится в степень B, то ее можно вынести за знак логарифма. Если основание логарифма возводится в степень A, за знак логарифма можно вынести число 1/A.
6
Если основание логарифма представлено некоторым выражением Q, содержащим переменную x, необходимо рассмотреть два случая: Q(x) ϵ (1;+∞) и Q(x) ϵ (0;1). Соответственно этому ставится и знак неравенства при переходе от логарифмического сравнения к простому алгебраическому.