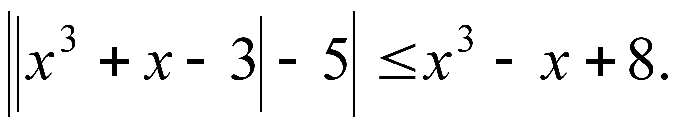Инструкция
1
Неравенства имеют как ряд уникальных особенностей, так и черты, сходные с уравнениями.
Одно из основных отличий накладывает как раз так знак "больше/меньше". Это означает, что при необходимости умножить обе части на какое-либо выражение (например, на знаменатель), мы должны четко знать его знак (и, конечно, тот факт, что оно не равно нулю). В частности, это нужно учитывать при возведении в квадрат - это ведь тоже умножение.
Посмотрим на просто примере. Очевидно, что 3<5. Умножим обе части на 2. 6<10. По-прежнему все верно. А теперь умножим на -2. Получим -12<-20. А вот это уже не верно. Просто так неравенства умножать на отрицательные числа или выражения нельзя. В этом случае знак неравенства нужно заменить на противоположный.
2
За исключением этого пункта, до определенного момента решаются неравенства так же, как и уравнения.

Приведение к общему знаменателю, поиск выколотых точек, перенос членов в левую часть, поиск корней и разложение на множители.
Вот. Дошли до этого самого "определенного момента": разложение на множители. Далее пути решения уравнений и неравенств расходятся.
3
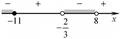
Будем применять для решения метод интервалов.
Рисуем числовую ось.
На ней отмечаем пустым кружочком и подписываем значения выколотых точек, а закрашенным - невыколотых, и начинаем узнавать знак неравенства в каждой из полученных областей. Для этого берем любую точку из этой области (лучше какую-нибудь удобную) и подставляем в неравенство на место x. В итоге получаем некоторое число. В зависимости от его знака пишем на числовой оси в данной области "+" или "-". Далее можно продолжить аналогичные действия для остальных областей, а можно и схитрить, так как есть некоторые закономерности для проставления знаков в методе интервалов: знаки областей чередуются при переходе через следующую точку, если соответствующее выражение с отмеченной на числовой оси точкой встречается в неравенстве нечетное количество раз, и не меняются при переходе через эту точку, если четное.
Выбираем из всех областей те, чей знак соответствует нашему неравенству.
4
В итоге получаем совокупность, которая в ответе записывается как "икс принадлежит..." - на месте многоточия стоят все подходящие области или точки. Выколотые точки на конце области обозначаются круглыми скобками - они не включаются в ответ, невыколотые - квадратными, и они включаются в ответ. Одиночные точки обозначаются фигурными скобками, а между областями и точками в ответе, так как это совокупность, ставится знак объединения ("U").
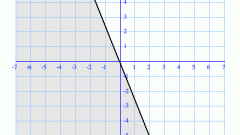
В неравенстве для двух переменных все аналогично, просто выполняется анализ значений не на числовой оси, а на плоскости.