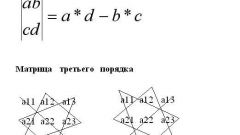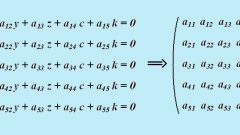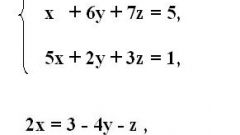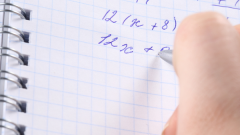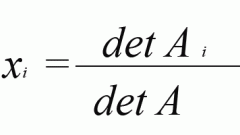Инструкция
1
Составьте заданные матрицы. Для этого впишите в скобки таблицу значений, которая имеет заданное число столбцов и строк, которые обозначаются n и m, соответственно. Если данные величины равны, то матрицу называют квадратной, если равны нулю, то матрица – нулевая.
2
Проведите главную диагональ матрицы, которая состоит из всех элементов таблицы, которые расположены на линии от левого верхнего угла до правого нижнего. Для того чтобы найти решение транспонирования матрицы, необходимо заменить элементы строк и столбцов относительно главной диагонали. К примеру, элемент а21 заменяется на элемент а12 и так далее. В итоге получится транспонированная матрица.
3
Проверьте, имеют ли две матрицы одинаковую размерность, т.е. величины m и n у них совпадают. В этом случае можно найти решение сложения заданных таблиц. Результатом суммирования будет новая матрица, каждый элемент которой равен сумме соответствующих элементов начальных матриц.
4
Сравните две заданные матрицы и определите, являются ли они согласованными. В этом случае число столбцов m первой таблицы, должно быть равно числу строк n второй. Если данное равенство соблюдается, то можно найти решение произведение заданных параметров.
5
Просуммируйте произведение каждого элемента строки первой матрицы на соответствующий элемент столбца второй матрицы. Результат запишите в первую верхнюю ячейку результирующей таблицы. Повторите все вычисления с остальными строками и столбцами матриц.
6
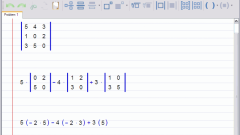
Найдите решение детерминанта заданной матрицы. Определитель может быть вычислен только в том случае, если таблица является квадратной, т.е. количество строк равно количеству столбцов. Его величина равна сумме произведения каждого элемента, находящегося в первой строке и j-ом столбце, на дополнительный минор к данному элементу и минус единицы в степени (1+j).
Видео по теме