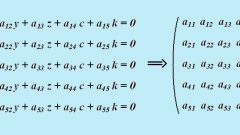Вам понадобится
- - ручка
- - бумага
Инструкция
1
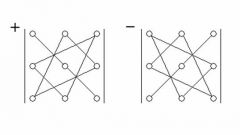
Известно, что определитель матрицы второго порядка вычисляется так: из произведения элементов главной диагонали вычитается произведение элементов побочной диагонали. Поэтому удобно разложить матрицу на миноры второго порядка и потом уже вычислить определители этих миноров, а также определитель исходной матрицы.
На рисунке представлена формула для вычисления определителя любой матрицы. Пользуясь ею, разложим матрицу сначала на миноры третьего порядка, а потом каждый полученный минор на миноры второго порядка, что позволит легко вычислить детерминант матриц.
На рисунке представлена формула для вычисления определителя любой матрицы. Пользуясь ею, разложим матрицу сначала на миноры третьего порядка, а потом каждый полученный минор на миноры второго порядка, что позволит легко вычислить детерминант матриц.
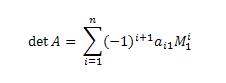
2
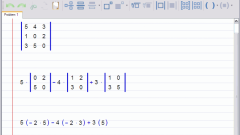
Разложим по формуле исходную матрицу на дополнительные матрицы размера 3 на 3. Дополнительные матрицы, или миноры, образуются вычеркиванием из исходной матрицы одной строки и одного столбца. В ряд многочленов такие миноры входят умноженными на тот элемент матрицы, к которому они являются дополнительным, знак многочлена определяется степенью -1, которая представляет собой сумму индексов элемента.

3
Теперь каждую из матриц третьего порядка раскладываем таким же образом на матрицы второго порядка. Находим определитель каждой такой матрицы и получим ряд многочленов из элементов исходной матрицы, дальше идут чисто арифметические вычисления.
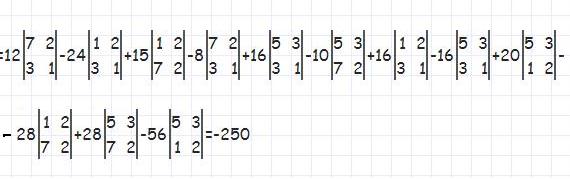
Видео по теме
Обратите внимание
Определитель можно вычислить только для квадратных матриц.
Разложение по столбцу/строке - это лишь один из способов вычисления детерминанта матрицы.
Разложение по столбцу/строке - это лишь один из способов вычисления детерминанта матрицы.
Полезный совет
Легко проверить количество конечных многочленов, вычислив факториал от числа столбцов\строк матрицы. Так для нашей матрицы порядка 4 конечных многочленов должно быть 4! = 24 штуки.
Если в матрице есть нулевые элементы, то целесообразно раскладывать ее по столбцу или строке, содержащей как можно больше нулей. Очевидно, что при этом некоторые дополнительные миноры будут умножены на ноль и могут не вычисляться.
Если в матрице есть нулевые элементы, то целесообразно раскладывать ее по столбцу или строке, содержащей как можно больше нулей. Очевидно, что при этом некоторые дополнительные миноры будут умножены на ноль и могут не вычисляться.
Источники:
- Нахождения определителя матрицы методом разложения по строке/столбцу в 2018