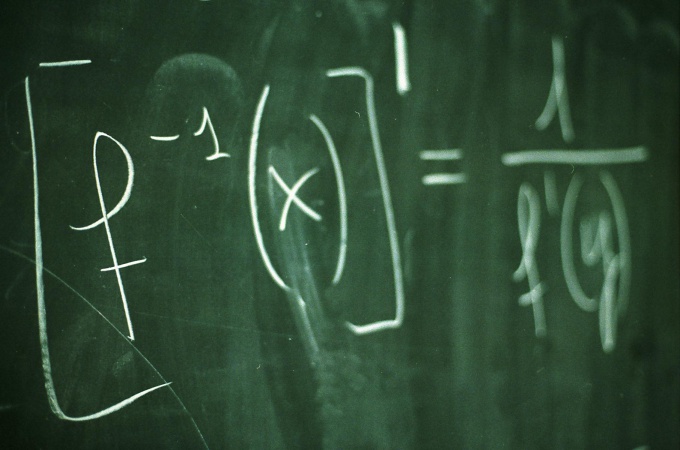Инструкция
1
Для быстрого вычисления производных первым делом выучите таблицу производных основных элементарных функций. Такая таблица производных представлена на рисунке. Затем определите к какому типу относится ваша функция. Если это простая функция от одного переменного, найдите ее в таблице и вычислите. Например, (√(x))′=1/(2×√(x)).
2
3
Если вам нужно найти производную суммы или разности двух функций, то вычислите производные каждого слагаемого, а затем сложите их, то есть (f(x)±g(x))′=(f(x))′±(g(x))′. Например, (x²+x³)′=(x²)′+(x³)′=2×x+3×x². Или, например, (2^x−sin(x))′=(2^x)′−(sin(x))′=2^x×ln2−cos(x).
4
Вычисляйте производную произведения двух функций по формуле (f(x)×g(x))′=f(x)′×g(x)+f(x)×g(x)′, то есть как сумму произведений производной первой функции на вторую функцию и производной второй функции на первую функцию. Например, (√(x)×tg(x))′=(√(x))′×tg(x)+√(x)×(tg(x))′=tg(x)/(2×√(x))+√(x)/cos²(x).
5
Если ваша функция представляет собой частное двух функций, то есть имеет вид f(x)/g(x), для вычисления ее производной используйте формулу (f(x)/g(x))′=(f(x)′×g(x)−f(x)×g(x)′)/(g(x)²). Например, (sin(x)/x)′=((sin(x)′)×x−sin(x)×x²)/x²=(cos(x)×x−sin(x))/x².
6
Если вам нужно вычислить производную сложной функции, то есть функции имеющей вид f(g(x)), аргументом которой является какая-либо зависимость, используйте следующее правило: (f(g(x)))′=(f(g(x))′×(g(x))′. Сначала возьмите производную по сложному аргументу, считая его простым, затем посчитайте производную сложного аргумента и результаты перемножьте. Таким способом вы найдете производную любой степени вложенности. Например, (sin(x)³)′=3×(sin(x))²×(sin(x))′=3×(sin(x))²×cos(x).
7
Если ваша задача вычислить производную высшего порядка, то вычисляйте последовательно производные низшего порядка. Например, (x³)′′=((x³)′)′=(3×x²)′=6×x.
Обратите внимание
Знак ′ обозначает взятие производной, а знак ^ – возведение в степень.