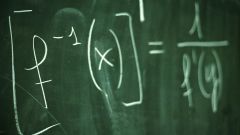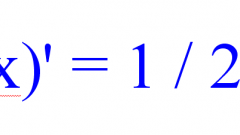Как найти производную от дроби

Появление дифференциального исчисления вызвано необходимостью решать конкретные физические задачи. Предполагается, что человек, владеющий дифференциальным исчислением, умеет брать производные от различных функций. Умеете ли вы брать производную от функции, выраженной дробью?

Инструкция

1. Любая дробь имеет числитель и знаменатель. В процессе нахождения производной от дроби потребуется находить отдельно производную числителя и производную знаменателя.
2. Чтобы найти производную от дроби, производную числителя домножьте на знаменатель. Вычтите из полученного выражения производную знаменателя, помноженную на числитель. Результат разделите на знаменатель в квадрате.
3. Пример 1[sin (x) / cos (x)]’ = [sin’ (x) · cos (x) — cos’ (x) · sin (x)] / cos? (x) = [cos (x) · cos (x) + sin (x) · sin (x)] / cos? (x) = [cos? (x) + sin? (x)] / cos? (x) = 1 / cos? (x).
4. Полученный результат является ничем иным, как табличным значением производной функции тангенса. Оно и понятно, ведь отношение синуса к косинусу и есть, по определению, тангенс. Итак,tg (x) = [sin (x) / cos (x)]' = 1 / cos? (x).
5. Пример 2[(x? — 1) / 6x]’ = [(2x · 6x — 6 · x?) / 6?] = [12x? — 6x?] / 36 = 6x? / 36 = x? / 6.
6. Частным случаем дроби является такая дробь, у которой в знаменателе единица. Найти производную от такого вида дроби проще: достаточно представить ее в виде знаменателя со степенью (-1).
7. Пример(1 / x)' = [x^(-1)]' = -1 · x^(-2) = -1 / x?.