Инструкция
1
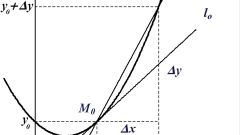
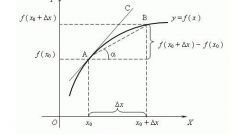
Рассмотрите неявную функцию, заданную некоторым уравнением. При этом невозможно выразить зависимость y(x) в явном виде. Приведите уравнение к виду F(x, y)=0. Чтобы найти производную y'(x) от неявной функции, сначала продифференцируйте уравнение F(x, y)=0 по отношению к переменной x, учитывая, что y дифференцируема по x. Используйте правила вычисления производной сложной функции.
2
Решите полученное после дифференцирования уравнение относительно производной y'(x). Итоговая зависимость и будет производной неявно заданной функции по переменной x.
3
Изучите пример для наилучшего понимания материала. Пусть функция задана в неявной форме как y=cos(x−y). Приведите уравнение к виду y−cos(x−y)=0. Продифференцируйте это уравнения по переменной x, применяя правила дифференцирования сложной функции. Получаем, y'+sin(x−y)×(1−y')=0, т.е. y'+sin(x−y)−y'×sin(x−y)=0. Теперь решите полученное уравнение относительно y': y'×(1−sin(x−y))=−sin(x−y). В итоге получается, что y'(x)=sin(x−y)÷(sin(x−y)−1).
4
Найдите производную неявной функции нескольких переменных следующим образом. Пусть задана функция z(x1, x2, …, xn) в неявной форме уравнением F(x1, x2,…, xn, z)=0. Найдите производную F'|x1, считая переменные x2, …, xn, z постоянными. Аналогично вычислите производные F'|x2, …, F'|xn, F'|z. После этого выразите частные производные в виде z'|x1=−F'|x1÷F'|z, z'|x2=−F'|x2÷F'|z, …, z'|xn=−F'|xn÷F'|z.
5
Рассмотрите пример. Пусть задана функция двух неизвестных z=z(x, y) формулой 2x²z−2z²+yz²=6x+6z+5. Приведите уравнение к виду F(x, y, z)=0: 2x²z−2z²+yz²−6x−6z−5=0. Найдите производную F'|x, считая y, z постоянными: F'|x=4xz−6. Аналогично, производная F'|y=z², F'|z=2x²-4z+2yz−6. Тогда z'|x=−F'|x÷F'|z=(6−4xz)÷(2x²−4z+2yz−6), а z'|y=−F'|y÷F'|z=−z²÷(2x²−4z+2yz−6).