Вам понадобится
- - минимальные данные, необходимые для решения задачи, а именно длина каждой стороны и диагонали пятиугольника;
- - калькулятор;
- - ручка;
- - лист бумаги.
Инструкция
1
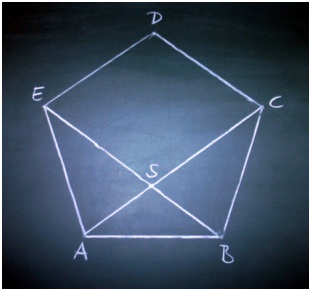
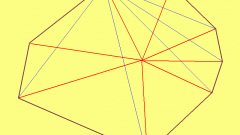
Внимательно прочитайте условие поставленной задачи. Руководствуясь им, нарисуйте на листе бумаги предполагаемый пятиугольник.
2
Обозначьте длину каждой из его сторон.
3
Проведите в пятиугольнике две диагонали. Обозначьте длину каждой диагонали.
4
Обратите внимание на то, что получилось в результате проведения диагоналей, и вы увидите, что они разбивают пятиугольник на три различных между собой треугольника.
5
Из вершины каждого треугольника проведите высоту к его основанию.
6
Измерьте длину высоты опущенной на основание для каждого треугольника.
7
Определите треугольников по формуле, приведенной ниже:
S = ½ × H × a,
где S – вычисляемая площадь треугольника;
H – высота каждого треугольника;
a – длина основания треугольника.
S = ½ × H × a,
где S – вычисляемая площадь треугольника;
H – высота каждого треугольника;
a – длина основания треугольника.
8
Вычислите площадь пятиугольника, сложив площади этих трех треугольников.
Обратите внимание
Помните, что правильным считается тот пятиугольник, у которого и все стороны, и все углы равны между собой. Если хотя бы одна сторона или угол отличается от других, то пятиугольник не считается правильным, и его площадь нельзя рассчитывать по упрощенной схеме.
Полезный совет
Проще всего определить площадь правильного пятиугольника. Для этого достаточно просто вычислить площадь одного из треугольников, а затем умножить ее на их количество. Ведь диагонали в правильном пятиугольнике разбивают его на треугольники одинаковой площади. Значительно упрощается задача и в том случае, если два угла пятиугольника являются прямыми. Достаточно провести одну диагональ, которая разобьет пятиугольник на треугольник и прямоугольник, площади которых можно найти совсем просто. Сумма вычисленных площадей будет равна площади самого пятиугольника.