Как начертить пятиугольник

Тема деления окружности на равные части с целью построения правильных вписанных многоугольников издавна занимала умы древних ученых. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах». Однако лишь спустя два тысячелетия эта задача была полностью решена не только графически, но и математически.

Инструкция

1. Приближенное построение правильного пятиугольника способом А. Дюрера, с помощью циркуля и линейки (через две окружности с общим радиусом, равным стороне пятиугольника).
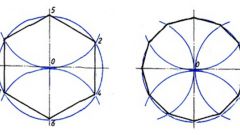
2. Построение правильного пятиугольника на основе правильного десятиугольника, вписанного в окружность (соединив вершины десятиугольника через одну).
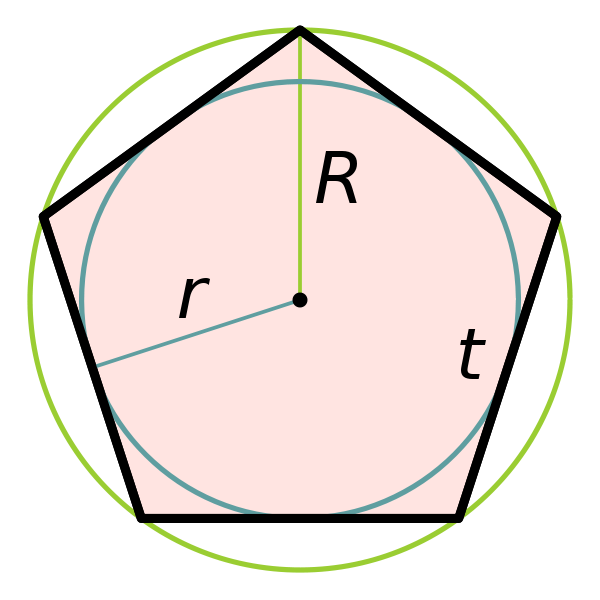
3. Графическое построение через вычисленный внутренний угол пятиугольника с помощью транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n - 2), т.к. у правильного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.
   
   А так же с помощью окружности и двух лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника.
4. Еще один простой графический способ: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.
   
   Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.
   
   Точки G,E,B,F,H – вершины правильного пятиугольника.
5. Построение с помощью приема Биона (позволяющего построить правильный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).
   
   Например: для n=5. Построим правильный треугольник ABC, где AB – диаметр заданной окружности. Найдем на AB точку D, по следующему соотношению: AD : AB = 2 : n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона правильного вписанного пятиугольника.
   
   При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся меньше 10,3%.
6. Построение по заданной стороне по методу Л. Да Винчи (используя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2 : ha =3/(n-1), которое можно выразить так: tg180°/n =3/(n-1)).
7. Общий способ построения правильных многоугольников по заданной стороне по методу Ф. Коваржика (1888 г.), на основе принципа Л. да Винчи.
   
   Единый способ построения правильного n-угольника на основании теоремы Фалеса.
   
   Можно добавить только, что приближенные методы построения многоугольников оригинальны, просты и красивы.