Вам понадобится
  • - циркуль;
  • - карандаш;
  • - линейка.
Инструкция
1
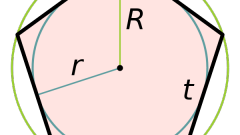
Чтобы построить правильный многоугольник со стороной m, вычислите радиус описанной около него окружности по формуле. Например, для правильного шестиугольника Рад.=m/(2∙sin180º/6)=m/(2∙sin30º), т.к. sin30º=1/2, получите: Рад.=m. Таким образом, искомый радиус равен стороне правильного шестиугольника.
2
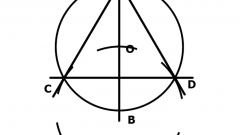
Начертите окружность с радиусом m. Отметьте на ней произвольную точку. Начиная от данной точки, разделите окружность на равные части, в зависимости от количества сторон в многоугольнике. Для этого раствором циркуля, равным стороне данного многоугольника, сделайте несколько засечек на окружности.
3
Например, для правильного шестиугольника необходимо разделить окружность на шесть равных частей. Соедините найденные точки последовательно отрезками, которые являются, по сути, хордами окружности. Вы построили правильный многоугольник.
4
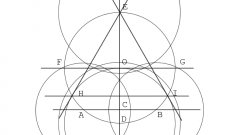
Существуют другие варианты построения правильных многоугольников. Пример 1. Постройте правильный треугольник со стороной m. Начертите произвольную прямую и отметьте на ней любую точку. От этой точки отложите при помощи циркуля отрезок, равный стороне треугольника m.
5
В верхней полуплоскости относительно заданной прямой проведите две полуокружности с радиусом m и центрами на концах построенного отрезка. Найдите точку пересечения полуокружностей. Соедините ее с концами отрезка. Вы начертили равносторонний треугольник.
6
Пример 2. Постройте квадрат со стороной m. Вычислите диагональ квадрата по формуле: Диаг.=m√2. Начертите произвольную прямую и отложите на ней отрезок, равный длине диагонали. Проведите две окружности с центрами на концах построенного отрезка и радиусом равным стороне квадрата m. Вы получите две точки пересечения окружностей. Соедините последовательно эти точки с концами отрезка. Вы начертили квадрат.