Инструкция
1
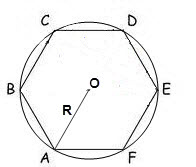
Если известен радиус окружности описанной около многоугольника, то его площадь можно вычислить по формуле:
S = (n/2)•R²•sin(2π/n), где n – число сторон многоугольника, R – радиус описанной окружности, π = 180º.
В правильном шестиугольнике все углы равны 120°, поэтому формула будет иметь вид:
S = √3 * 3/2 * R²
S = (n/2)•R²•sin(2π/n), где n – число сторон многоугольника, R – радиус описанной окружности, π = 180º.
В правильном шестиугольнике все углы равны 120°, поэтому формула будет иметь вид:
S = √3 * 3/2 * R²
2
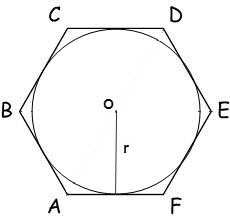
В случае, когда окружность с радиусом r вписана в многоугольник, его площадь вычисляется по формуле:
S = n * r² * tg(π/n), где n – число сторон многоугольника, r – радиус вписанной окружности, π = 180º.
Для шестиугольника эта формула принимает вид:
S = 2 * √3 * r²
S = n * r² * tg(π/n), где n – число сторон многоугольника, r – радиус вписанной окружности, π = 180º.
Для шестиугольника эта формула принимает вид:
S = 2 * √3 * r²
3
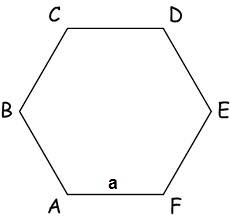
Площадь правильного многоугольника так же можно вычислить, зная лишь длину его стороны по формуле:
S = n/4 * a² * ctg(π/n), n – число сторон многоугольника, a – длина стороны многоугольника, π = 180º.
Соответственно площадь шестиугольника равна:
S = √3 * 3/2 * a²
S = n/4 * a² * ctg(π/n), n – число сторон многоугольника, a – длина стороны многоугольника, π = 180º.
Соответственно площадь шестиугольника равна:
S = √3 * 3/2 * a²
Источники:
- площадь шестигранника формула