Инструкция
1
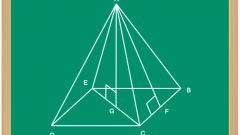
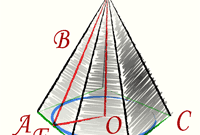
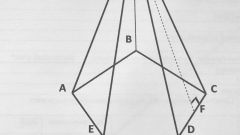
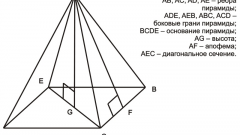
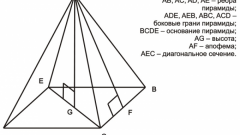
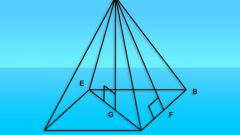
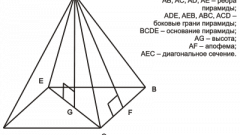
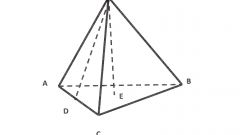
Полная площадь поверхности любого многогранника складывается из суммы площадей его граней. В правильной четырехугольной пирамиде они представлены двумя формами многоугольников - в основании лежит квадрат, в боковые поверхности имеют треугольную конфигурацию. Начните расчеты, например, с вычисления площади четырехугольного основания пирамиды (Sₒ). По определению правильной пирамиды в ее основании должен лежать правильный многоугольник, в данном случае - квадрат. Если в условиях приведена длина ребра основания (a), просто возведите его во вторую степень: Sₒ = a². Если известна только длина диагонали основания (l), для вычисления площади найдите половину ее квадрата: Sₒ = l²/2.
2
Определите площадь треугольной боковой грани пирамиды Sₐ. Если известна длина ее общего с основанием ребра (a) и апофема (h), рассчитайте половину от произведения этих двух величин: Sₐ = a*h/2. При указанных в условиях длинах бокового ребра (b) и ребра основания (a) найдите половину произведения длины основания на корень из разницы между возведенной в квадрат длиной бокового ребра и четвертью квадрата длины основания: Sₐ = ½*a*√(b²-a²/4). Если кроме длины общего с основанием ребра (a) дан плоский угол в вершине пирамиды (α), вычислите отношение возведенной в квадрат длины ребра к удвоенному косинусу половины плоского угла: Sₐ = a²/(2*cos(α/2)).
3
Рассчитав площадь одной боковой грани (Sₐ), увеличьте полученную величину в четыре раза, чтобы вычислить площадь боковой поверхности правильной четырехугольной пирамиды. При известной апофеме (h) и периметре основания (P) это действие вместе со всем предыдущим шагом можно заменить вычислением половины произведения этих двух параметров: 4*Sₐ = ½*h*P. В любом случае, полученную площадь боковой поверхности сложите с рассчитанной на первом шаге площадью квадратного основания фигуры - это и будет полная площадь поверхности пирамиды: S = Sₒ+4*Sₐ.