Вам понадобится
- Бумага, ручка, калькулятор
Инструкция
1
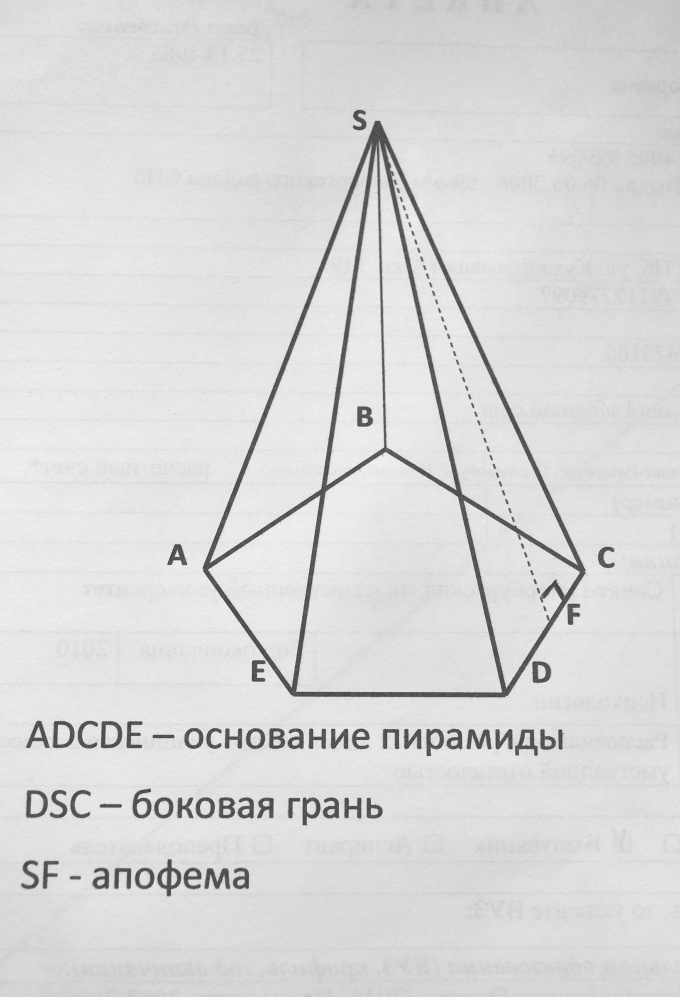
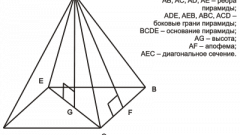
Сначала вычислим площадь боковой поверхности пирамиды. Под боковой поверхностью подразумевается сумма площадей всех боковых граней. Если вы имеете дело с правильной пирамидой (то есть такой, в основании которой лежит правильный многоугольник, а вершина проецируется в центр этого многоугольника), то для вычисления всей боковой поверхности достаточно умножить периметр основания (то есть сумму длин всех сторон многоугольника, лежащего в основании пирамиды) на высоту боковой грани (иначе называемой апофемой) и разделить полученное значение на 2: Sб=1/2P*h, где Sб - это площадь боковой поверхности, P - периметр основания, h - высота боковой грани (апофема).
2
Если же перед вами произвольная пирамида, то придется отдельно вычислять площади всех граней, а затем их складывать. Поскольку боковыми гранями пирамиды являются треугольники, воспользуйтесь формулой площади треугольника: S=1/2b*h, где b - это основание треугольника, а h - высота. Когда площади всех граней вычислены, остается только сложить их, чтобы получить площадь боковой поверхности пирамиды.
3
Затем необходимо вычислить площадь основания пирамиды. Выбор формулы для расчета зависит от того, какой многоугольник лежит в основании пирамида: правильный ( то есть такой, все стороны которого имеют одинаковую длину) или неправильный. Площадь правильного многоугольника можно вычислить, умножив периметр на радиус вписанной в многоугольник окружности и поделив полученное значение на 2: Sn=1/2P*r, где Sn - это площадь многоугольника, P - это периметр, а r - это радиус вписанной в многоугольник окружности.
4
Если в основании пирамиды лежит неправильный многоугольник, то для вычисления площади всей фигуры снова придется разбивать многоугольник на треугольники, вычислять площадь каждого, а затем складывать.
5
Чтобы завершить вычисление площади поверхности пирамиды, сложите площади боковой поверхности и основания пирамиды.
Видео по теме