Инструкция
1
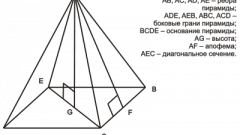
Пирамида – это многогранник, в основании которого лежит многоугольник. Боковые грани представляют собой треугольники с общей вершиной, которая является одновременно вершиной пирамиды. Если в основании пирамиды лежит правильный многоугольник, т.е. такой, у которого все углы и все стороны равны, то пирамида называется правильной. Поскольку в условии задачи не указывается, какой именно многогранник следует рассматривать в данном случае, можно считать, что имеет место правильная n-угольная пирамида.
2
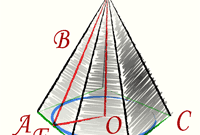
В правильной пирамиде все ребра равны между собой, все грани - равные равнобедренные треугольники. Высотой пирамиды является перпендикуляр, опущенный из вершины на ее основание.
3
Нахождение высоты пирамиды зависит от того, что дано в условии задачи. Применяйте формулы, в которых для нахождения каких–либо параметров пирамиды используется ее высота. К примеру, дано: V – объем пирамиды; S – площадь основания. Используйте формулу нахождения объема пирамиды V=SH/3, где H – высота пирамиды. Отсюда следует: H=3V/S.
4
Двигаясь в том же направлении, следует отметить, что если площадь основания не дана, ее в некоторых случаях можно найти по формуле нахождения площади правильного многоугольника. Введите обозначения:р - полупериметр основания (полупериметр легко найти, если известно число сторон и величина одной стороны);h – апофема многоугольника (апофемой называется перпендикуляр, опущенный из центра многоугольника на любую из его сторон); а - сторона многоугольника;n – число сторон.Таким образом, p=an/2, а S=ph= (an/2)h. Откуда следует: H=3V/ (an/2) h.
5
Разумеется, существует множество других вариантов. К примеру, дано:h - апофема пирамиды;n - апофема основания;H - высота пирамиды.Рассмотрите фигуру, образованную высотой пирамиды, ее апофемой и апофемой основания. Она представляет собой прямоугольный треугольник. Решите задачу с помощью всем известной теоремы Пифагора. Применительно к данному случаю можно записать: h²=n²+H², откуда H²=h²-n². Вам остается лишь извлечь квадратный корень из выражения h²-n².