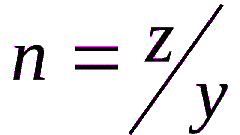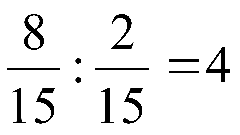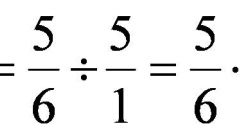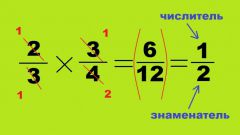Инструкция
1
Если делителем тоже является обыкновенная дробь, то начните с ее инвертирования: поменяйте местами числитель и знаменатель. Затем замените знак деления знаком умножения, а все дальнейшие вычисления производите по правилам перемножения двух обыкновенных дробей. Например, если надо разделить 9/16 на 6/8, то записать действие этого шага можно так: 9/16 : 6/8 = 9/16 * 8/6.
2
Сократите числители и знаменатели обеих дробей-множителей, если есть возможность подобрать для них общий делитель. На этот делитель (целое число) надо разделить и числитель и знаменатель. В примере из предыдущего шага числитель первой дроби (9) и знаменатель второй (6) имеют общий делитель 3, а для знаменателя первой (16) и числителя второй (8) таким делителем будет цифра 8. После соответствующего сокращения запись действия примет такой вид: 9/16 : 6/8 = 9/16 * 8/6 = 3/1 * 1/2.
3
Перемножьте попарно числители и знаменатели полученных в результате сокращения дробей - рассчитанное значение и будет искомым результатом. Например, использованный выше образец после этого шага можно будет записать так: 9/16 : 6/8 = 9/16 * 8/6 = 3/2 * 1/2 = (3*1)/(2*2) = 3/4.
4
Если число, стоящее в числителе полученного результата больше числа в его знаменателе, то такая форма записи называется «неправильной» обыкновенной дробью и ее следует перевести в «смешанный» формат. Для этого разделите числитель на знаменатель, полученное целое значение запишите перед дробью, остаток от деления поставьте в числитель, а знаменатель оставьте в прежнем виде. Например, если бы полученный после предыдущего шага результат был равен 9/4, то его следовало бы привести к виду 2 1/4.
Видео по теме
Полезный совет
Если делителем является целое число или десятичная дробь, то его сначала следует перевести в формат обыкновенной дроби, а затем действовать по описанному выше алгоритму. Например, целое число 40 надо записать как 40/1, а десятичную дробь 3,14 - как 314/100.