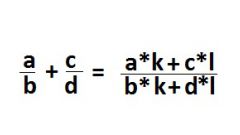Вам понадобится
  • - калькулятор;
  • - бумага;
  • - карандаш.
Инструкция
1
Сначала вспомните что дробь – это всего лишь условная запись деления одного числа на другое. В отличие от сложения и умножения, при делении двух целых чисел не всегда получается целое число. Вот и договорились называть эти два «делящихся» числа дробью. То число, которое делят, назвали числителем, а то, на которое делят - знаменателем.
2
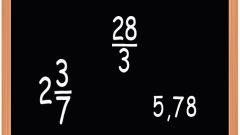
Чтобы записать дробь, напишите сначала ее числитель, затем проведите под этим числом горизонтальную черту, а под чертой напишите знаменатель. Горизонтальная черта, разделяющая числитель и знаменатель, называется дробной чертой. Иногда ее изображают в виде наклонной черты «/» или «∕». При этом, числитель записывается слева от черты, а знаменатель справа. Так, например, дробь «две третьих» запишется как 2/3. Для наглядности числитель обычно пишут в верхней части строки, а знаменатель - в нижней, то есть вместо 2/3 можно встретить: ⅔.
3
Если числитель дроби больше ее знаменателя, то такую «неправильную» дробь обычно записывают в виде «смешанной» дроби. Чтобы получить из неправильной дроби смешанную, просто разделите числитель на знаменатель и запишите полученное частное. После чего поместите остаток от деления в числитель дроби и запишите эту дробь справа от частного (знаменатель не трогайте). Например, 7/3 = 2⅓.
4
Чтобы сложить две дроби с одинаковым знаменателем, просто сложите их числители (знаменатели не трогайте). Например, 2/7 + 3/7 = (2+3)/7 = 5/7. Аналогично производите и вычитание двух дробей (числители при этом вычитаются). Например, 6/7 – 2/7 = (6-2)/7 = 4/7.
5
Чтобы сложить две дроби с разными знаменателями, умножьте числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби – на знаменатель первой. В итоге у вас получится сумма двух дробей с одинаковыми знаменателями, сложение которых описано в предыдущем пункте.

Например, 3/4 + 2/3 = (3*3)/(4*3) + (2*4)/(3*4) = 9/12 + 8/12 = (9+8)/12 = 17/12 = 1 5/12.
6
Если знаменатели дробей имеют общие делители, то есть делятся на одно и то же число, выберите в качестве общего знаменателя наименьшее число, делящееся на первый и второй знаменатель одновременно. Так, например, если первый знаменатель равен 6, а второй 8, то в качестве общего знаменателя возьмите не их произведение (48), а число 24, которое делится как на 6, так и на 8. Числители дробей при этом умножаются на частное от деления общего знаменателя на знаменатель каждой дроби. Например, для знаменателя 6 таким числом будет 4 – (24/6), а для знаменателя 8 – 3 (24/8). Более наглядно этот процесс виден на конкретном примере:

5/6 + 3/8 = (5*4)/24 + (3*3)/24 = 20/24 + 9/24 = 29/24 = 1 5/24.

Вычитание дробей с разными знаменателями производится совершенно аналогично.
7
Чтобы умножить две дроби, перемножьте между собой их числители и знаменатели.
Например, 2/3 * 4/5 = (2*4)/(3*5) = 8/15.
8
Чтобы разделить две дроби, умножьте первую дробь на перевернутую (обратную) вторую дробь.
Например, 2/3 : 4/5 = 2/3 * 5/4 = 10/12.
9
Чтобы сократить дробь, разделите ее числитель и знаменатель на одно и то же число. Так например, результат предыдущего примера (10/12) можно записать как 5/6:
10/12 = (10:2)/(12:2) = 5/6.