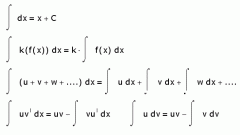Инструкция
1
Четко усвойте, что интегрирование - процесс, обратный дифференцированию. В большинстве учебников функция, получаемая в результате интегрирования, обозначается как F(x) и носит название первообразной. Производная первообразной равна F'(x)=f(x). Например, если в задаче дана функция f(x)=2x, процесс интегрирования выглядит следующим образом:
∫2x=x^2+C, где C=const, при условии, что F'(x)=f(x)
Процесс интегрирования функции можно записать и иным образом:
∫f(x)=F(x)+C
2
Обязательно запомните следующие свойства интегралов:
1. Интеграл суммы равен сумме интегралов:
∫[f(x)+z(x)]=∫f(x)+∫z(x)
Для доказательства этого свойства возьмите производные от левой и правой части интеграла, после чего используйте аналогичное свойство суммы производных, пройденное вами ранее.
2. Постоянный множитель выносится за знак интеграла:
∫AF(x)=A∫F(x), где A=const.
3
Простые интегралы вычисляются с использованием специальной таблицы. Однако, чаще всего в условиях задач встречаются сложные интегралы, для решения которых знания таблицы недостаточно. Приходится прибегать к использованию ряда дополнительных методов. Первый из них заключается в интегрировании функции путем ее подведения под знак дифференциала:
∫f(d(x)z'(x)dx=∫f(u)d(u)
Под u подразумевается сложная функция, которая и преобразовывается в простую.
4
Существует также несколько более сложный метод, который обычно применяется в случае, если необходимо проинтегрировать сложную тригонометрическую функцию. Он заключается в интегрировании по частям. Выглядит это следующим образом:
∫udv=uv-∫vdu
Представьте себе, например, что дан интеграл ∫x*sinx dx. Обозначьте х как u, а dv - как sinxdx. Соответственно, v=-cosx, а du=1 Подставляя эти значения в вышеуказанную формулу, получите следующее выражение:
∫x*sinxdx=-x *cosx-∫(-cosx)=sinx-x*cosx+C, где С=const.
5
Еще один метод заключается в замене переменной. Он применяется в том случае, если под знаком интеграла имеются выражения со степенями или корнями. Формула замены переменной обычно имеет следующий вид:
[∫f(x)dx]=∫f[z(t)]z'(t)dt, причем, t=z(t)