Как вычислить приближенно интеграл

Классические модели приближенного вычисления определенного интеграла основаны но построении интегральных сумм. Эти суммы должны быть наиболее короткими, но обеспечивающими достаточно малую погрешность вычисления. Зачем? С тех пор, как появились серьезные ЭВМ и хорошие ПК, актуальность задачи сокращения числа вычислительных операций несколько отошла на второй план. Безусловно, огульно отвергать их не следует, а вот взвесить между простотой алгоритма (где много вычислительных операций) и сложностью более точного - явно не помешает.

Инструкция

1. Рассмотрим задачу вычисления определенных интегралов методом «Монте-Карло». Применение стало возможным после появления первых ЭВМ, поэтому его отцами считаются американцы Нейман и Улам (отсюда и броское название, так как по тем временам наилучшим датчиком случайных чисел являлась игровая рулетка). От авторского права (в названии) отойти не имею права, но сейчас упоминают либо статистические испытания, либо статистическое моделирование.
2. Для получения случайных чисел, обладающих заданным распределением на интервале (a, b) используются случайные числа z, равномерных на (0, 1). В среде Pascal это соответствует подпрограмме Random. На калькуляторах на этот случай имеется кнопка RND. Существуют и таблицы таких случайных чисел. Этапы моделирования простейших распределений также просты (буквально до крайности). Так, порядок вычисления числовой модели случайной на (a,b) величины, плотность вероятности которой W(x) следующая. Определив функцию распределения F(x), приравняйте ее zi. Тогда xi=F^(-1)(zi) (имеется в виду обратная функция). Далее получайте сколь угодно много (в пределах возможностей вашего ПК) значений цифровой модели xi.
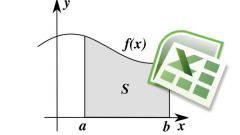
3. Теперь следует непосредственный этап вычислений. Пусть вам необходимо вычислить определенный интеграл (см. рис. 1а). На рисунке 1 W(x) можно считать произвольной плотностью вероятности случайной величины (СВ), распределенной на (a,b), а искомый интеграл – математическим ожиданием функции этой СВ. Так что единственное требование к требование к W(x) – условие нормировки (рис. 1b).
   В математической статистике оценкой математического ожидания является среднее арифметическое наблюдаемых значений функции СВ (рис.1 с). Вместо наблюдений наберите их цифровые модели и вычисляйте определенные интегралы с практически с любой желаемой точностью без всяких (иной раз тяжелейших, если привлечь метод Чебышева) выкладок.
   
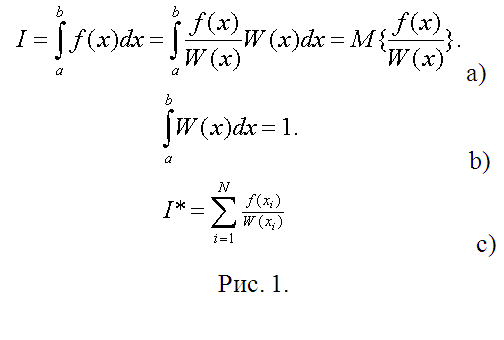
4. Вспомогательную W(x) следует брать простейшей, но, все-таки таки, хотя бы слегка напоминающей (по графику) интегрируемую функцию. Не возможно скрыть, что снижение погрешности в 10 раз стоит увеличения выборки модели в 100 раз. Ну и что? Когда кому-либо требовалось более трех знаков за запятой? А это всего лишь миллион вычислительных операций.