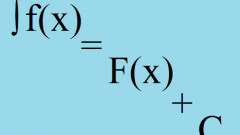Инструкция
1
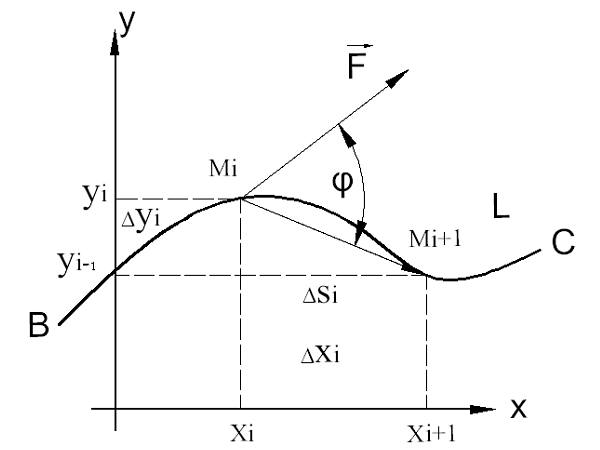
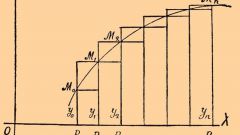
Пусть на кривой в декартовой системе координат определена функция F(x, y). Для интегрирования функции кривая разбивается на отрезки длиной, близкой к 0. Внутри каждого такого отрезка выбираются точки Mi с координатами xi, yi, определяются значения функции в этих точках F(Mi) и умножаются на длины участков:F(M1)·∆s1 + F(M2)·∆s2 + … F(Mn)·∆sn = ΣF(Mi)·∆si при 1 ≤ I ≤ n.
2
Полученная сумма называется криволинейной интегральной суммой. Соответствующий интеграл равен пределу от этой суммы:∫F(x, y)ds = lim ΣF(Mi)·∆si = lim ΣF(xi, yi)· √ ((∆xi)² + (∆yi)²) = lim F(xi, yi)·√(1 + (∆yi/∆xi) ²)·∆xi = ∫F(x, y)·√(1 + (y’)²)dx.
3
Пример.Найдите криволинейный интеграл ∫x²·yds вдоль линии y = ln x при 1 ≤ x ≤ e.Решение.По формуле:∫x²yds = ∫x²·√(1 + ((ln x)’)²) = ∫x²·√(1 + 1/x²) = ∫x² ·√((1 + x²)/x) = ∫x·√(1 + x²)dx = 1/2·∫√(1 + x²)d(1 + x²) = ½·(1 + x)^3/2 = [1 ≤ x ≤ e] = 1/3·((1 + e²)^3/2 - 2^3/2) ≈ 7,16.
4
Пусть кривая задана в параметрической форме x = φ(t), y = τ(t). Чтобы вычислить криволинейный интеграл, применим уже известную формулу:∫F(x, y)ds = lim ΣF(Mi)·∆si = lim ΣF(xi, yi)·√((∆xi)² + (∆yi)²).
5
Подставив значения x и y, получим:∫F(x, y)ds = lim Σ F(φ(ti), τ(ti))·√(φ² (ti) + τ² (ti))·∆ti = ∫F(φ(t), τ(t))·√(φ² + τ²)dt.
6
Пример.Вычислите криволинейный интеграл ∫y²ds, если линия задана параметрически: x = 5·cos t, y = 5·sin t при 0 ≤ t ≤ π/2.Решение.ds = (25·cos² t + 25·sin² t)dt = 5dt.∫y²ds = ∫25·sin²t·5dt = 125/2∫(1 – cos 2t)dt = 125/2·(t – sin 2t/2) = [0 ≤ t ≤ π/2] = 125/2·((π/2 - 0) – (0 - 0)) = 125/2·π/2 = 125·π/4.