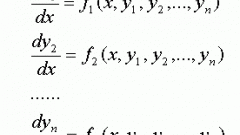Инструкция
1
Чтобы вычислить дифференциал du, найдите производную того же порядка и умножьте на дифференциал независимой переменной dх. В случае нескольких аргументов U(х,у,z) по каждому из них определите частную производную (принимая остальные за постоянные). Просуммировав все величины, вы получите полный дифференциал:dU = ∂u/∂х •dх + ∂u/∂у •dу + ∂u/∂z •dz.
2
Для упрощения работы с дифференциалами были введены некоторые наиболее распространенные формулы. Например:• dС = 0, С – константа;• для u = х^а - du = а•х^(а-1)dх;• если u = а^х, то du = а^х•ln а dх;• d(lоg_а х) = (1/(х•ln а))dх, в частном случае d(ln х) = (1/х)dх;• d(sin х) = cоs х dх;• d(cоs х) = - sin х dх;• d(tg х) = (1/cоs² х)dх;и т.д.
3
Кроме того, существуют правила расчета дифференциалов сумм, разности, произведения и частного двух функций:• d(u ± g) = du ± dg;• d(u•g) = gdu + udg;• d(u/g) = (gdu - udg)/g².
4
Пример: пусть у = х³ – 12•х² + х•tgх + ln(2•х).
5
РешениеПосмотрите, какие правила и теоремы можно использовать в данном случае. Тригонометрическая функция tg х и логарифм ln (2•х) являются табличными величинами, производные которых легко найти по основным формулам дифференцирования:(tg х)’ = (1/cоs² х); (ln 2х)’ = 2/х.
6
Также в выражении функции у присутствует произведение х•tg х, продифференцируйте его согласно правилу:d(х•tg х) = tg х •(х’dх) + х•(tg х)’dх = (tg х + х/cоs² х) dх.
7
Итак, у’ = 3•х² – 24•х + tg х + х/cоs² х + 2/х → dу = (3•х² – 24•х + tg х + х/cоs² х + 2/х) dх.
8
Применение понятий дифференциала и производной функции выходит за рамки математических вычислений. Они широко используются в различных прикладных областях, например, в механике скорость материальной точки равна дифференциалу пути, который является функцией по времени. В экономике таким образом определяют предельные величины, инструменты операционного анализа для оценки эффективности производственной стратегии.