Инструкция
1
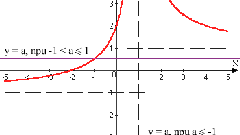
Чтобы вычислить предел в заданной точке x0, следует подставить это значение аргумента в выражение функции, стоящее под знаком lim. Вовсе не обязательно, чтобы эта точка принадлежала области определения функции. Если предел определен и равен однозначному числу, то говорят, что функция сходится. Если же он не может быть определен, или бесконечен в конкретной точке, то налицо расхождение.
2
Теорию решения пределов лучше совмещать с практическими примерами. Например, найдите предел функции:lim (х² – 6•х - 14)/(2•² + 3•х - 6) при х→-2.
3
Решение.Подставьте в выражение значение х = -2:lim (х² – 6•х - 14)/(2•х² + 3•х - 6) = -1/2.
4
Не всегда решение является настолько очевидным и простым, особенно если выражение слишком громоздкое. В этом случае сначала следует упростить его методами сокращения, группировки или замены переменной:lim_(х→-8) (10•х - 1)/(2•х + ∛x) = [у= ∛x] = lim_(у→-2) (10•у³ - 1)/(2•у³ + у) = 9/2.
5
Часто возникают ситуации невозможности определения предела, особенно если аргумент стремится к бесконечности или нулю. Подстановка не приносит ожидаемого результата, приводя к неопределенности вида [0/0] или [∞/∞]. Тогда применимо правило Лопиталя-Бернулли, которое предполагает нахождение первой производной. Например, вычислите предел lim (х² – 5•х -14)/(2•х²+ х - 6) при х→-2.
6
Решение.lim (х² – 5•х -14)/(2•х² + х - 6) = [0/0].
7
Найдите производную:lim (2•х - 5)/(4•х + 1) = 9/7.
8
Для того, чтобы облегчить работу, в некоторых случаях можно применять так называемые замечательные пределы, представляющие собой доказанные тождества. На практике их существует несколько, однако чаще всего используются два.
9
lim (sinx/x) = 1 при x → 0, верно и обратное: lim (x/sinx) = 1; x → 0.Аргумент может быть любой конструкцией, главное, чтобы ее значение стремилось к нулю:lim (x³ – 5•x² + x)/sin(x³ – 5•x² + x) = 1; x → 0.
10
Второй замечательный предел:lim (1 + 1/x)^x = e (число Эйлера) при x → ∞.
Видео по теме