Инструкция
1
Параллелепипед имеет одну особенность, не свойственную другим фигурам. Его грани попарно параллельны и имеют равные измерения и числовые характеристики, такие как площадь и периметр. Любую пару таких граней можно принять за основания, тогда оставшиеся будут составлять его боковую поверхность.
2
Можно найти длины рёбер параллелепипеда по диагонали, однако одной этой величины мало. Во-первых, обратите внимание на то, какая разновидность этой пространственной фигуры вам дана. Это может быть правильный параллелепипед, обладающий прямыми углами и равными измерениями, т.е. куб. В этом случае будет достаточно знать длину одной диагонали. Во всех остальных случаях должен быть, как минимум, еще один известный параметр.
3
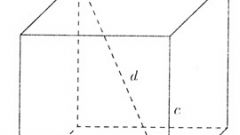
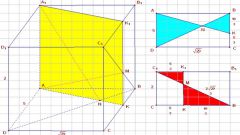
Диагонали и длины сторон в параллелепипеде связаны определенным соотношением. Эта формула вытекает из теоремы косинусов и представляет собой равенство суммы квадратов диагоналей и суммы квадратов ребер:
d1² + d2² + d3² + d4² = 4•а² + 4•b² + 4•c², где а – длина, b – ширина и c - высота.
d1² + d2² + d3² + d4² = 4•а² + 4•b² + 4•c², где а – длина, b – ширина и c - высота.
4
5
Пример: найти длину стороны куба, если его диагональ равна 5 см.
Решение.
25 = 3•а²
а = 5/√3.
Решение.
25 = 3•а²
а = 5/√3.
6
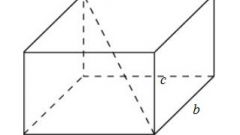
Рассмотрим прямой параллелепипед, у которого боковые ребра перпендикулярны основаниям, а сами основания являются параллелограммами. Его диагонали попарно равны и связаны с длинами ребер по следующему принципу:
d1² = а² + b² + c² + 2•а•b•cos α;
d2² = а² + b² +c² – 2•а•b•cos α, где α – острый угол между сторонами основания.
d1² = а² + b² + c² + 2•а•b•cos α;
d2² = а² + b² +c² – 2•а•b•cos α, где α – острый угол между сторонами основания.
7
Этой формулой можно воспользоваться, если известны, к примеру, одна из сторон и угол или эти величины могут быть найдены по другим условиям задачи. Решение упрощается, когда все углы в основании прямые, тогда:
d1² + d2² = 2•а² + 2•b² + 2•c².
d1² + d2² = 2•а² + 2•b² + 2•c².
8
Пример: найдите ширину и высоту прямоугольного параллелепипеда, если ширина b больше длины а на 1 см, высота c – в 2 раза больше, а диагональ d – в 3.
Решение.
Запишите основную формулу квадрата диагонали (в прямоугольном параллелепипеде они равны):
d² = а² + b² + c².
Решение.
Запишите основную формулу квадрата диагонали (в прямоугольном параллелепипеде они равны):
d² = а² + b² + c².
9
Выразите все измерения через заданную длину а:
b = а + 1;
c = а•2;
d = а•3.
Подставьте в формулу:
9•а² = а² + (а + 1)² + 4•а²
b = а + 1;
c = а•2;
d = а•3.
Подставьте в формулу:
9•а² = а² + (а + 1)² + 4•а²
10
Решите квадратное уравнение:
3•а² – 2•а – 1 = 0
Найдите длины всех ребер:
а = 1; b = 2; c = 2.
3•а² – 2•а – 1 = 0
Найдите длины всех ребер:
а = 1; b = 2; c = 2.
Источники:
- формула суммы длин всех рёбер параллелепипеда