Инструкция
1
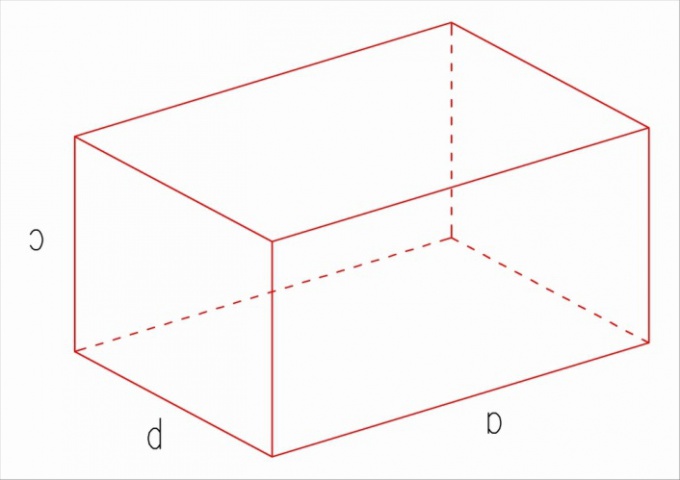
Полная площадь поверхности параллелепипеда складывается из площади его боковой поверхности и площади его оснований.
Как говорилось выше, противоположные грани параллелепипеда попарно равны между собой. Следовательно, полную поверхность параллелепипеда можно определить как удвоенную сумму площадей разных граней:
S = 2(So + Sб1 + Sб2), где Sо – площадь основания параллелепипеда; Sб1, Sб2 – площади смежных боковых граней параллелепипеда.
В общем случае, и основания параллелепипеда, и его боковые грани являются параллелограммами. Учитывая, что площадь параллелограмма можно без труда найти по любой из двух нижеприведенных формул, поиск полной площади поверхности параллелепипеда не вызовет сложностей.
Как говорилось выше, противоположные грани параллелепипеда попарно равны между собой. Следовательно, полную поверхность параллелепипеда можно определить как удвоенную сумму площадей разных граней:
S = 2(So + Sб1 + Sб2), где Sо – площадь основания параллелепипеда; Sб1, Sб2 – площади смежных боковых граней параллелепипеда.
В общем случае, и основания параллелепипеда, и его боковые грани являются параллелограммами. Учитывая, что площадь параллелограмма можно без труда найти по любой из двух нижеприведенных формул, поиск полной площади поверхности параллелепипеда не вызовет сложностей.
Видео по теме
Полезный совет
Площадь параллелограмма можно найти по любой из формул:
1) S = ½ah, где а – основание параллелограмма; h – его высота;
2) S = ½ab∙sinα, где a,b – длины сторон параллелограмма, α – острый угол между ними.
1) S = ½ah, где а – основание параллелограмма; h – его высота;
2) S = ½ab∙sinα, где a,b – длины сторон параллелограмма, α – острый угол между ними.