Инструкция
1
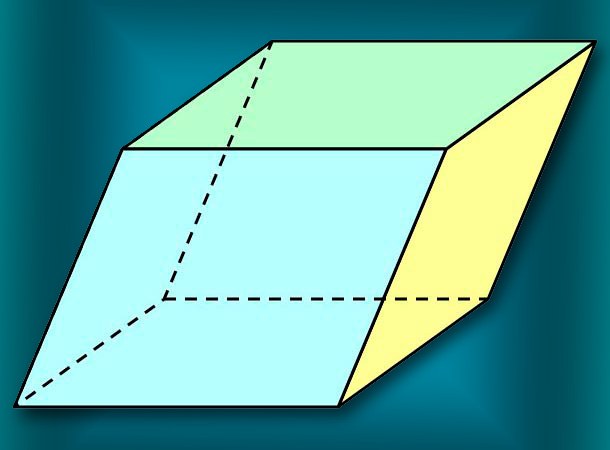
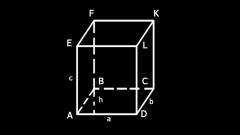
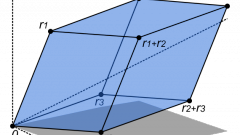
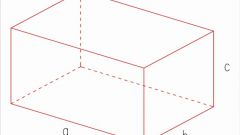
Начните с вычисления площади основания (S) параллелепипеда. Противоположные стороны четырехугольника, образующего эту плоскость объемной фигуры, по определению должны быть параллельны, а угол между ними может быть любым. Поэтому площадь грани определите умножением длин ее двух смежных ребер (a и b) на синус угла (?) между ними: S=a*b*sin(?).
2
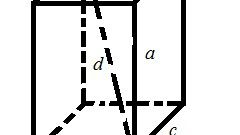
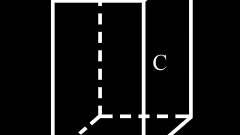
Умножьте полученное значение на длину ребра параллелепипеда (с), образующего общий трехмерный угол со сторонами a и b. Так как боковая грань, которой принадлежит это ребро, по определению не обязательно должна быть перпендикулярна основанию параллелепипеда, то рассчитанное значение умножьте еще и на синус угла наклона (?) боковой грани: V=S*c*sin(?). В общем виде формулу вычисления объема произвольного параллелепипеда можно записать так: V=a*b*c*sin(?)*sin(?). Например, пусть в основании параллелепипеда лежит грань, ребра которой имеют длины 15 и 25 сантиметров и угол между ними в 30°, а боковые грани наклонены на 40° и имеют ребро, длиной в 20см. Тогда объем этой фигуры будет равен 15*25*20*sin(30°)*sin(40°) ? 7500*0,5*0,643 ? 2411,25см?.
3
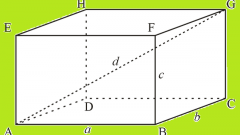
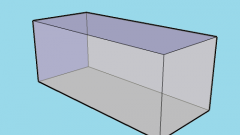
Если нужно вычислить объем прямоугольного параллелепипеда, то формулу можно значительно упростить. В силу того, что синус 90° равен единице, поправки на углы можно убрать из формулы, а значит, будет достаточно перемножить длины трех смежных ребер параллелепипеда: V=a*b*c. Например, для фигуры с длинами ребер, использованными в примере на предыдущем шаге, объем составит 15*25*20 = 7500см?.
4
Еще более проста формула для вычисления объема куба - прямоугольного параллелепипеда, все ребра которого имеют одинаковую длину. Возведите длину этого ребра (a) в куб, чтобы получить искомое значение: V=a?. Например, у прямоугольного параллелепипеда, длины всех ребер которого равны 15см, объем будет равен 153=3375см?.
Видео по теме