Как найти сторону квадрата, если известен периметр

Периметром называют общую длину всех сторон геометрической фигуры. Обычно его находят методом сложения размеров сторон. В случае с правильным многоугольником периметр можно найти, умножив длину отрезка между вершинами на количество таких отрезков. Именно к такому виду многоугольников относится квадрат. Зная его периметр, можно с помощью одного лишь арифметического действия найти длину его стороны.

Вам понадобится

• -калькулятор.

Инструкция

1. Рассмотрите любой квадрат. Вспомните его свойства. У него 4 стороны, причем все они одинаковы по длине и расположены по отношению друг к другу под прямым углом. Обозначьте сторону квадрата как а, а периметр — как р.
2. Вспомните, как найти размер части любого объекта, если эти части равны, а количество их вам известно. Это можно сделать, разделив целое на количество частей. Представьте периметр как целый объект, тогда каждая сторона будет его частью. Всего этих частей четыре. То есть размер стороны можно найти, разделив периметр на 4. Выразить это можно формулой a=p/4.
3. Точно таким же образом, зная периметр, можно найти размер стороны любого правильного многоугольника. Для пятиугольника справедлива формула а=р/5, для шестиугольника — а=р/6 и т. д.
4. Подумайте, у какого еще многоугольника 4 стороны, и при том они равны между собой. Это ромб, частным случаем которого многие математики считают квадрат. У ромба углы, принадлежащие одной стороне, не равны между собой, но для вычисления периметра это не играет никакой роли. Сторону любого ромба можно найти точно так же, как и сторону квадрата, то есть разделив периметр на 4.
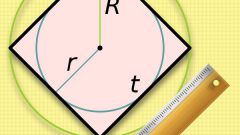
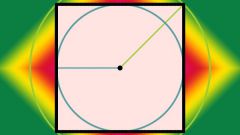
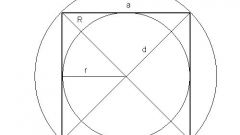
5. Зная периметр квадрата, можно найти еще несколько размеров, важных для этой геометрической фигуры. Сделайте дополнительное построение, вписав в квадрат окружность. Проведите диаметр так, чтобы он соединил точки касания окружности с противолежащими сторонами квадрата. Диаметр равен стороне этой геометрической фигуры. А это значит, что и его можно найти точно тем же способом, то есть разделив периметр на 4. Выразить это можно формулой d=p/4.
6. В задачах очень часто требуется не диаметр окружности, а ее радиус. Найти его можно, разделив диаметр на 2. А если попытаться выразить радиус через периметр, получится формула r=d/2=(p:4)/2=р/8.
7. Через периметр можно выразить и радиус описанной окружности. Постройте ее и проведите радиус, который пересечет окружность в одной из вершин квадрата. Из центра окружности проведите перпендикуляр к одной из сторон данного угла. У вас получился прямоугольный треугольник, у которого к тому же равны катеты, а один еще и является радиусом вписанной окружности, то есть его размер равен р/8. Радиус описанной окружности представляет собой гипотенузу этого треугольника, и найти ее можно по теореме Пифагора, то есть R^2=(p/8)^2+(p/8)^2=2(p/8)^2.