Вам понадобится
- Калькулятор
Инструкция
1
Допустим, нам известны длины диагоналей ромба. Как найти длину стороны ромба?
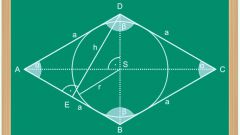
Так как диагонали ромба (AC, BD) пересекаются под прямым углом и делятся точкой пересечения (O) пополам, то сторона ромба (AB) будет диагональю прямоугольного треугольника (ABO) с катетами, образованными половинками диагоналей ромба (AO, BO). Тогда по теореме Пифагора получается: квадрат длины стороны ромба равняется сумме квадратов половин длин его диагоналей.
|AB|^2=|AO|^2+|BO|^2=(|AC|/2)^2+(|BD|/2)^2.
Соответственно, длина стороны ромба будет равняться корню квадратному из суммы квадратов половинок его диагоналей.
|AB|=√((|AC|/2)^2+(|BD|/2)^2).
Пусть нам известны площадь ромба (ABCD) и его высота (BH), т.е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае?
Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты.
|AB|=S/|BH|
Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам.
Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла.
В виде формулы эта зависимость будет выглядеть следующим образом:
|AB|= (|AC|/2)/sin(α/2), где α - величина угла BAD.
Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры - длина противоположной углу диагонали, соотношение диагоналей и т.д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию - косинус, тангенс и т.п.
Так как диагонали ромба (AC, BD) пересекаются под прямым углом и делятся точкой пересечения (O) пополам, то сторона ромба (AB) будет диагональю прямоугольного треугольника (ABO) с катетами, образованными половинками диагоналей ромба (AO, BO). Тогда по теореме Пифагора получается: квадрат длины стороны ромба равняется сумме квадратов половин длин его диагоналей.
|AB|^2=|AO|^2+|BO|^2=(|AC|/2)^2+(|BD|/2)^2.
Соответственно, длина стороны ромба будет равняться корню квадратному из суммы квадратов половинок его диагоналей.
|AB|=√((|AC|/2)^2+(|BD|/2)^2).
Пусть нам известны площадь ромба (ABCD) и его высота (BH), т.е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае?
Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты.
|AB|=S/|BH|
Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам.
Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла.
В виде формулы эта зависимость будет выглядеть следующим образом:
|AB|= (|AC|/2)/sin(α/2), где α - величина угла BAD.
Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры - длина противоположной углу диагонали, соотношение диагоналей и т.д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию - косинус, тангенс и т.п.