Инструкция
1
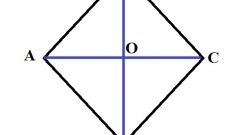
Если кроме длины одной из диагоналей (l) о рассматриваемом четырехугольнике известно, что он является частным случаем ромба - квадратом, никаких расчетов производить не придется. В этом случае длины обеих диагоналей одинаковы - просто приравняйте искомую величину (L) к известной: L=l.
2
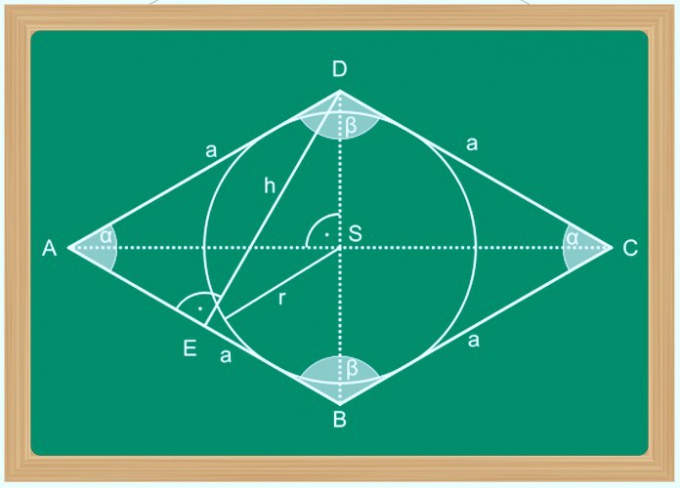
Знание длины стороны ромба (a) в дополнение к длине одной из диагоналей (l) позволит рассчитать длину другой (L) по теореме Пифагора. Это возможно потому, что две половины пересекающихся диагоналей образуют со стороной ромба прямоугольный треугольник. Половины диагоналей в нем являются катетами, а сторона - гипотенузой, поэтому равенство, вытекающее из теоремы Пифагора можно записать так: a² = (l/2)² + (L/2)². Для использования в расчетах преобразуйте его к такому виду: L = √(4*a²-l²).
3
При известной величине одного из углов (α) ромба и длине одной из диагоналей (l) для нахождения величины другой (L) рассмотрите тот же прямоугольный треугольник. Тангенс половины известного угла в нем будет равен отношению длины противолежащего катета - половины диагонали l - к прилежащему - половине диагонали L: tg(α/2) = (l/2)/(L/2) = l/L. Поэтому для вычисления искомой величины используйте формулу L = l/tg(α/2).
4
Если в условиях задачи приведена длина периметра (P) ромба и размер его диагонали (l), формулу вычисления длины второй (L) можно свести к равенству, использованному во втором шаге. Для этого разделите периметр на четверку и замените этим выражением длину стороны в формуле: L = √(4*(P/4)²-l²) = √(P²/4-l²).
5
В исходных условиях кроме длины одной из диагоналей (l) может быть приведена и площадь (S) фигуры. Тогда для вычисления длины второй диагонали ромба (L) используйте очень простой алгоритм - удвойте площадь и разделите полученное значение на длину известной диагонали: L = 2*S/l.