Как найти основание равнобедренного треугольника по двум сторонам

Треугольник - это геометрическая фигура, которая имеет минимально возможное для многоугольников количество сторон и вершин и поэтому является простейшей фигурой, в которой присутствуют углы. Можно сказать, что это самый «заслуженный» многоугольник в истории математики - он использовался для выведения большого числа тригонометрических функций и теорем. И среди этих элементарных фигур есть более простые и менее. К первым относится равнобедренный треугольник, состоящий из одинаковых боковых сторон и основания.

Инструкция

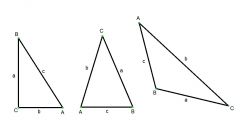
1. Найти длину основания такого треугольника по боковым сторонам без дополнительных параметров можно только в том случае, если они заданы своими координатами в двух- или трехмерной системе. Например, пусть даны трехмерные координаты точек A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃), отрезки между которыми образуют боковые стороны. Тогда вам известны и координаты третьей стороны (основания) - ее образует отрезок AC. Для вычисления его длины найдите разницу между координатами точек вдоль каждой оси, полученные значения возведите в квадрат и сложите, а из результата извлеките квадратный корень: AC = √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).
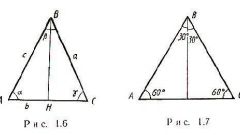
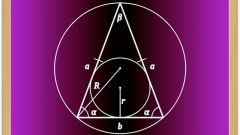
2. Если же известна только длина каждой из боковых сторон (a), то для вычисления длины основания (b) нужна дополнительная информация - например, величина угла между ними (γ). В этом случае можно воспользоваться теоремой косинусов, из которой вытекает, что длина стороны треугольника (не обязательно равнобедренного) равна квадратному корню из суммы квадратов длин двух других сторон, из которой вычтено удвоенное произведение их длин на косинус угла между ними. Так как в равнобедренном треугольнике длины задействованных a формуле сторон одинаковы, то ее можно упростить: b = a*√(2*(1-cos(γ))).
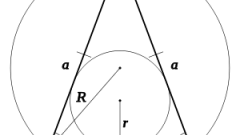
3. При тех же исходных данных (длина боковых сторон равна a, угол между ними равен γ) можно использовать и теорему синусов. Для этого найдите удвоенное произведение известной длины стороны на синус половины угла, лежащего напротив основания треугольника: b = 2*a*sin(γ/2).
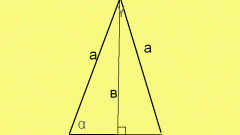
4. Если кроме длин боковых сторон (a) дана величина угла (α), прилегающего к основанию, то можно применить теорему о проекциях: длина стороны равна сумме произведений двух других сторон на косинус угла, который каждая из них образует с этой стороной. Так как в равнобедренном треугольнике эти стороны, как и задействованные углы, имеют одинаковую величину, то записать формулу можно так: b = 2*a*cos(α).