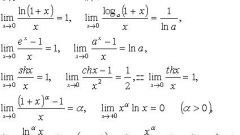Как определить предел функции

В математических справочниках дается несколько определений предела функции. Например, одно из них: число А может называться пределом функции f(x) в точке a, если анализируемая функция определена в окрестности точки а (за исключением самой точки а), при этом для каждого значения ε>0 должно быть такое δ>0, чтобы все х, удовлетворяющие условиям |x–a|

Вам понадобится

• - математический справочник;
• - простой карандаш;
• - тетрадь;
• - линейка;
• - ручка.

Инструкция

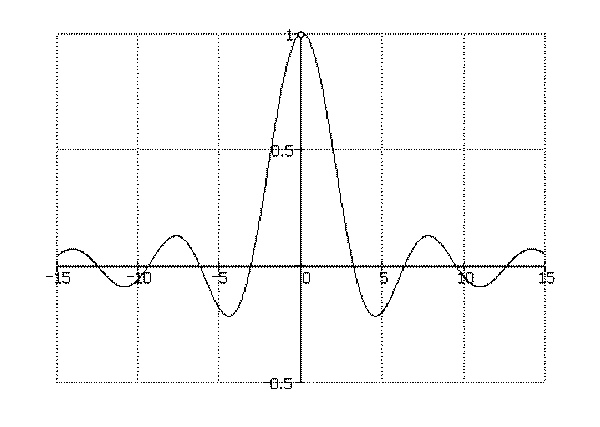
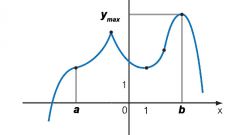
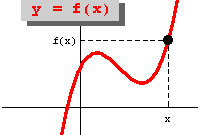
1. Представьте, что независимая переменная х стремится к числу а. Зная это, вы можете присвоить х любое значение, близкое к а, но не само а. При этом используется следующее обозначение: x→a. Допустим, значение функции f(x) также стремится к некому числу b: в этом случае b будет пределом функции.
2. Введите строгое определение предела f(x). В результате этого получится, что функция y=f(x) устремляется к пределу b при x→a, при условии, что для любого положительного числа ε может быть указано такое положительное число δ, чтобы при всех x, не равных a, из области определения данной функции справедливым было неравенство |f(x)-b|
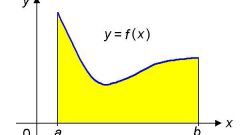
3. Изобразите наглядно полученное неравенство. Поскольку из неравенства |x-a|
4. Обратите внимание на то, что предел анализируемой функции обладает свойствами, которые присущи числовой последовательности, то есть lim C = C при x, стремящейся к a. Другими словами, такая функция имеет предел, однако он единственный.