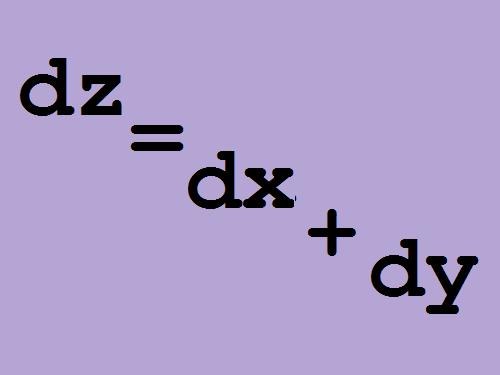Инструкция
1
Дифференциал (от лат. «разность») – это линейная часть полного приращения функции. Дифференциал принято обозначать df, где f – функция. Функцию одного аргумента иногда изображают dxf или dxF. Предположим, есть функция z = f(x, y), функция двух аргументов x и y. Тогда полное приращение функции будет иметь вид:
f(x, y) – f(x_0, y_0) = f’_x (x, y)*(x – x_0) + f’_y(x ,y)*(y – y_0) + α, где α – бесконечно малая величина (α → 0), которая игнорируется при определении производной, поскольку lim α = 0.
f(x, y) – f(x_0, y_0) = f’_x (x, y)*(x – x_0) + f’_y(x ,y)*(y – y_0) + α, где α – бесконечно малая величина (α → 0), которая игнорируется при определении производной, поскольку lim α = 0.
2
Дифференциал функции f по аргументу x является линейной функцией относительно приращения (x – x_0), т.е. df(x_0) = f'_x_0 (Δx).
3
Геометрический смысл дифференциала функции: если функция f дифференцируема в точке x_0, то ее дифференциал в этой точке есть приращение ординаты (y) касательной линии к графику функции.
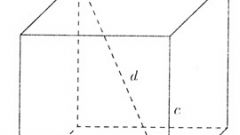
Геометрический смысл полного дифференциала функции двух аргументов – это трехмерный аналог геометрического смысла дифференциала функции одного аргумента, т.е. это приращение аппликаты (z) касательной плоскости к поверхности, уравнение которой задано дифференцируемой функцией.
Геометрический смысл полного дифференциала функции двух аргументов – это трехмерный аналог геометрического смысла дифференциала функции одного аргумента, т.е. это приращение аппликаты (z) касательной плоскости к поверхности, уравнение которой задано дифференцируемой функцией.
4
Можно записать полный дифференциал функции через приращения функции и аргументов, это более общепринятая форма записи:
Δz = (δz/δx)dx + (δz/δy)dy, где δz/δx – производная функции z по аргументу x, δz/δy – производная функции z по аргументу y.
Говорят, что функция f(x, y) дифференцируема в точке (x, y), если при таких значениях x и y можно определить полный дифференциал этой функции.
Выражение (δz/δx)dx + (δz/δy)dy и есть линейная часть приращения исходной функции, где (δz/δx)dx – дифференциал функции z по x, а (δz/δy)dy – дифференциал по y. При дифференцировании по одному из аргументов предполагается, что другой аргумент или аргументы (если их несколько) - постоянные величины.
Δz = (δz/δx)dx + (δz/δy)dy, где δz/δx – производная функции z по аргументу x, δz/δy – производная функции z по аргументу y.
Говорят, что функция f(x, y) дифференцируема в точке (x, y), если при таких значениях x и y можно определить полный дифференциал этой функции.
Выражение (δz/δx)dx + (δz/δy)dy и есть линейная часть приращения исходной функции, где (δz/δx)dx – дифференциал функции z по x, а (δz/δy)dy – дифференциал по y. При дифференцировании по одному из аргументов предполагается, что другой аргумент или аргументы (если их несколько) - постоянные величины.
5
Пример.
Найдите полный дифференциал следующей функции: z = 7*x^2 + 12*y - 5*x^2*y^2.
Решение.
Используя предположение, что y – постоянная величина, найдите частную производную по аргументу x,
δz/δx = (7*x^2 + 12*y - 5*x^2*y^2)’dx = 7*2*x + 0 – 5*2*x*y^2 = 14*x – 10*x*y^2;
Используя предположение, что x – постоянная величина, найдите частную производную по аргументу y:
δz/δy = (7*x^2 + 12*y - 5*x^2*y^2)’dy = 0 + 12 – 5*2*x^2*y = 12 – 10x^2*y.
Найдите полный дифференциал следующей функции: z = 7*x^2 + 12*y - 5*x^2*y^2.
Решение.
Используя предположение, что y – постоянная величина, найдите частную производную по аргументу x,
δz/δx = (7*x^2 + 12*y - 5*x^2*y^2)’dx = 7*2*x + 0 – 5*2*x*y^2 = 14*x – 10*x*y^2;
Используя предположение, что x – постоянная величина, найдите частную производную по аргументу y:
δz/δy = (7*x^2 + 12*y - 5*x^2*y^2)’dy = 0 + 12 – 5*2*x^2*y = 12 – 10x^2*y.
6
Запишите полный дифференциал функции:
dz = (δz/δx)dx + (δz/δy)dy = (14*x – 10*x*y^2)dx + (12 – 10x^2*y).
dz = (δz/δx)dx + (δz/δy)dy = (14*x – 10*x*y^2)dx + (12 – 10x^2*y).
Обратите внимание
В какой-то точке функции могут быть определены частные производные по одному из аргументов, но при этом дифференциал может не существовать для совокупности этих значений.
Источники:
- найти функцию по её дифференциалу