Инструкция
1
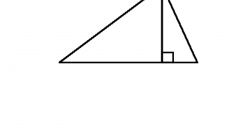
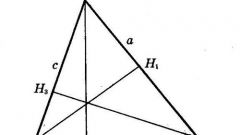
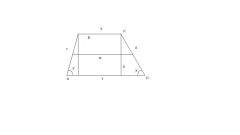
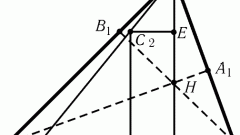
Из трех высот треугольника наименьшей будет та, которая опущена на самую большую из сторон фигуры. Чтобы убедиться в этом, выразите все три высоты треугольника через размеры его сторон и сравните. Пусть из трех сторон a, b, c произвольного остроугольного треугольника сторона а — наибольшая, сторона с — наименьшая. Обозначим ha высоту, опущенную на сторону а, hb высоту, проведенную к стороне b, hc — высоту на сторону с. Высота делит любой треугольник на два прямоугольных треугольника, в которых эта высота всегда будет одним из катетов.
2
Высота ha, проведенная к наибольшей стороне а, может быть определена по теореме Пифагора: hа²= b² - а₁² или hа²=с² - а₂². Где а₁ и а₂ — отрезки, на которые сторона а разделена высотой hа. Также по теореме Пифагора выразите две другие высоты треугольника через его стороны:
hb ²= a²-b₁² или hb²= c²-b₂²; hc²=a²-c₁² или hc²=b²-c₂².
hb ²= a²-b₁² или hb²= c²-b₂²; hc²=a²-c₁² или hc²=b²-c₂².
3
Из сравнения формул, определяющих высоты треугольника, очевидно, что соотношение между уменьшаемым и вычитаемым дает наименьшую разность в выражениях hа²= b² - а₁² и hа²=с²-а₂², поскольку вычитаемые а₁ и а₂ — отрезки наибольшей стороны треугольника.
4
Определить меньшую высоту треугольника можно также через синус известного угла треугольника. Если по условию задан наибольший из углов, то этот угол лежит против наибольшей стороны, и именно из него проведена наименьшая высота. Чтобы избежать громоздких вычислений, лучше выразите искомую высоту через тригонометрические функции двух других углов треугольника, поскольку отношение стороны треугольника к синусу противолежащего угла — величина для данного треугольника постоянная. Следовательно, наименьшая высота треугольника ha=b*SinB или ha=c*SinC, где В -угол между наибольшей стороной а и стороной b, а С — угол между наибольшей стороной а и стороной с треугольника.
Видео по теме