Вам понадобится
  • - радиус полуокружности;
  • - линейка;
  • - циркуль;
  • - лист бумаги;
  • - карандаш;
  • - формула площади круга.
Инструкция
1
Постройте окружность с заданным радиусом. Центр ее обозначьте как О. Чтобы получить полукруг, достаточно провести через эту точку отрезок до пересечения с окружностью. Этот отрезок является диаметром данной окружности и равен двум ее радиусам. Вспомните, что такое окружность и что такое круг. Окружность - это линия, все точки которой удалены от центра на одинаковое расстояние. Круг - часть плоскости, ограниченная этой линией.
2
Вспомните формулу площади круга. Она равна квадрату радиуса, умноженному на постоянный коэффициент π, равный 3,14. То есть площадь круга выражается формулой S=πR2, где S – площадь, а R - радиус окружности. Вычислите площадь полукруга. Она равна половине площади круга, то есть S1= πR2/2.
3
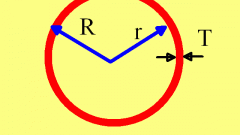
В случае, когда вам в условиях дана только длина окружности, найдите сначала радиус. Длина окружности вычисляется по формуле P=2πR. Соответственно, чтобы найти радиус, необходимо длину окружности разделить на удвоенный коэффициент. Получается формула R=P/2π.
4
Полукруг можно представить и как сектор. Сектором называется часть круга, которая ограничена его двумя радиусами и дугой. Площадь сектора равна площади круга, умноженной на отношение центрального угла к полному углу окружности. То есть, в данном случае она выражается формулой S=π*R2*n°/360°. Угол сектора известен, он составляет 180°. Подставив его значение, вы снова получите ту же самую формулу - S1= πR2/2.