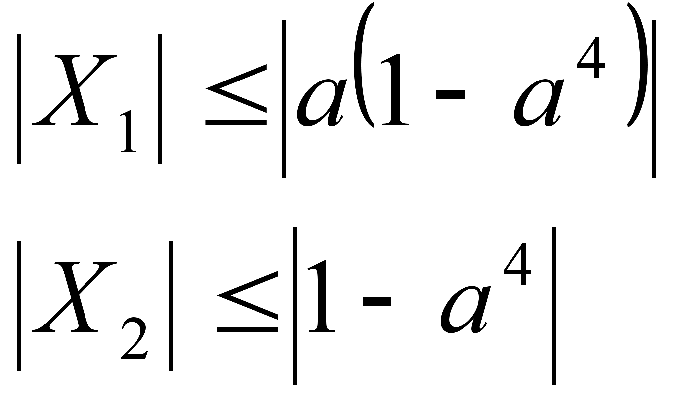Инструкция
1
С параметрами могут быть как уравнения, так и неравенства. В том и другом случае нам нужно выразить икс.
Просто в таком типе примеров это будет сделано не явно, а через этот самый параметр.
Сам по себе параметр, точнее, его значение - это число. Обычно параметры обозначают буквой а. Но проблема в том, что мы не знаем ни его модуля, ни знака. Отсюда возникают трудности при работе с неравенствами или раскрытии модулей.
Просто в таком типе примеров это будет сделано не явно, а через этот самый параметр.
Сам по себе параметр, точнее, его значение - это число. Обычно параметры обозначают буквой а. Но проблема в том, что мы не знаем ни его модуля, ни знака. Отсюда возникают трудности при работе с неравенствами или раскрытии модулей.
2
Тем не менее, можно (но осторожно, предварительно отметив все возможные ограничения) применять все обычные методы работы с уравнениями и неравенствами.
И, в принципе, само выражение х через а обычно не отнимает много времени и сил.
А вот написание полного ответа - это куда более кропотливый и трудоемкий процесс.
И, в принципе, само выражение х через а обычно не отнимает много времени и сил.
А вот написание полного ответа - это куда более кропотливый и трудоемкий процесс.
3
Дело в том, что в связи с незнанием значения параметра, мы обязаны рассмотреть все возможные случаи для всех значений а от минус до плюс бесконечности.
Тут нам очень пригодится графический метод. Иногда его еще называют "раскраска". Он заключается в том, что мы в осях х(а) (или а(х) - как удобнее) изображаем линии, полученные в результате преобразования нашего исходного примера. И далее начинаем работать с этими линиями: так как значение а не является фиксированным, то нам нужно линии, содержащие в своем уравнении параметр смещать по графику, параллельно отслеживая и высчитывая точки пересечения с другими линиями, а также анализируя знаки областей: подходят они нам или нет. Подходящие для удобства и наглядности будем заштриховывать.
Таким образом, мы проходим всю числовую ось от минус до плюс бесконечности, проверив ответ для всех а.
Тут нам очень пригодится графический метод. Иногда его еще называют "раскраска". Он заключается в том, что мы в осях х(а) (или а(х) - как удобнее) изображаем линии, полученные в результате преобразования нашего исходного примера. И далее начинаем работать с этими линиями: так как значение а не является фиксированным, то нам нужно линии, содержащие в своем уравнении параметр смещать по графику, параллельно отслеживая и высчитывая точки пересечения с другими линиями, а также анализируя знаки областей: подходят они нам или нет. Подходящие для удобства и наглядности будем заштриховывать.
Таким образом, мы проходим всю числовую ось от минус до плюс бесконечности, проверив ответ для всех а.
4
Сам же ответ записывается аналогично ответу для метода интервалов с некоторой оговоркой: мы не просто указываем совокупность решений для х, а пишем, какому множеству значений а соответствует какое множество значений х.