Как измерять параметры

В тех случаях, когда речь идет об измерениях, главное – получение величины, обладающей минимальной погрешностью. С математической точки зрения – определенного параметра, имеющего максимальную точность. Для этого используют критерии выбора оценки.

Инструкция

1. Пояснения приведены на основе оптимального измерения амплитуды радиоимпульса, которая хорошо укладывается в рамки математического подхода к решению задачи и рассматривалась в статистической радиотехнике.
2. Все сведения об измеряемом параметре содержатся в его апостериорной плотности вероятности, которая пропорциональна функции правдоподобия, умноженной на априорную плотность. Если априорная плотность вероятности неизвестна, то вместо апостериорной плотности используется функция правдоподобия.
3. Предположите, что на прием пришла реализация вида x(t)=S(t, λ)+n(t), где S(t, λ) детерминированная функция времени t, а λ параметр. n(t) гауссовский белый шум с нулевым средним и известными характеристиками. На приемной стороне λ воспринимается как случайная величина. Уравнение правдоподобия для определения оценки параметров сигнала по методу максимума функционала правдоподобия имеет вид d/dλ•{∫(0, T)•[x(t)- S(t, λ)]^2•dt}=0. (1)Здесь интеграл, берется от нуля до T (T – время наблюдения).
4. Составьте уравнение правдоподобия (1), положив длительность радиоимпульса равной времени наблюдения T, а S(t, λ)=λcosωt (радиоимпульс). d/dλ•{∫(0, T)[x(t)- λcosωt)]^2•dt]}=0.Найдите корни этого уравнения и примите их за оценочные значения амплитуды:d/dλ•{∫(0, T)[x(t)- λ•cosωt)]^2dt}=-2•{∫(0, T)•[x(t)- λ•cosωt)]•cosωt•dt]}=-2•∫(0, T)[x(t)•cosωt)]dt+2λ•∫(0, T)(cosωt)^2•dt=0.
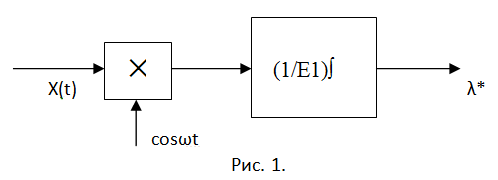
5. Тогда оценка λ*=(1/E1)•∫(0, T)[x(t)•cosωt)]•dt, где Е1=∫(0, T)(cosωt)^2•dt – энергия радиоимпульса с единичной амплитудой. На основании этого выражения постройте структурную схему оптимального (по максимуму правдоподобия) измерителя амплитуды радиоимпульса (см. рис. 1).
   
6. Для того чтобы окончательно убедиться в правильности выбора оценки, проверьте ее на несмещенность. Для этого найдите ее математическое ожидание и убедитесь, что совпадает с истинным значением параметра. M[λ*]=M[*=(1/E1)•∫(0,T)[x(t)•cosωt)]dt=(1/E1)•M{∫(0,T)[λ•cosωt+n(t)]cosωt•dt}= =(1/E1)•∫(0,T)[λ•(cosωt)^2+0]dt =λ.Оценка несмещенная.