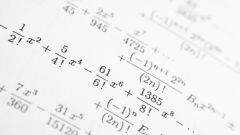Как решать уравнения с х

Ещё древнегреческий математик Диофант Александрийский для указания неизвестного числа ввел буквенные обозначения. Самое частое в ряду неизвестных - икс, его мы ставим по умолчанию, каждый раз составляя уравнение или неравенство. Хотя можем использовать любой другой не цифровой символ. Уравнения, в которых кроме чисел только одно неизвестное – икс, и способы их решения, мы сейчас и рассмотрим.

Инструкция

1. Решить уравнение - значит, найти все его корни. Корень уравнения, то есть значение неизвестного, при котором уравнение становится верным, может быть один или нет. Корней может быть несколько, бесконечное число или не быть вовсе.
2. Имеет значение при решении уравнения область определения функции. Дело в том, что при некоторых значениях x уравнение теряет смысл. Так, к примеру, знаменатель не может быть равен нулю, так что если в уравнении есть дроби с участием x в знаменателе, то область допустимых значений ограничена. Первый шаг при решении любого уравнения - определить его область допустимых значений. Помните: у корня четной степени не может быть отрицательное подкоренное выражение, знаменатель не может быть равен нулю, тригонометрические функции имеют собственные ограничения и т.д.
3. В процессе решения уравнения, мы упрощаем его, постепенно сводя к более легкому для нас, но с теми же корнями уравнению. Мы можем переносить слагаемые уравнения с одной стороны знака равно на другую, изменяя знак минус на плюс и наоборот. Можем обе части уравнения умножить, разделить или изменить как-то иначе, но обязательно симметрично, то есть одинаково и правую, и левую части уравнения. Можем раскрывать скобки и выносить за них. Выполнять арифметические действия, указанные в уравнении, согласно правилам. Собственно в этом и состоит процесс решения. Привести уравнение к «приличному» виду и потом узнать его корни.
4. Первыми в школьном курсе рассматриваются линейные уравнения с одной неизвестной. Уравнения эти имеют в общем случае вид: ax+b=0. Здесь a и b обозначения для числовых значений. Решение уравнения выглядит так: x=-b/a. Получив для решения сложно выглядящее уравнение, мы пытаемся в придать ему привычный вид линейного. Для чего, если в уравнении есть дробные выражения, приводим все слагаемые уравнения к общему знаменателю. После чего умножаем обе части уравнения на данный знаменатель. Раскрываем все скобки. Переносим все слагаемые включающие в себя x на одну сторону уравнения. Все без неизвестного на противоположную. Складываем, вычитаем, выполняем все требуемые и возможные действия. Которые обычно приводят нас к тому, что с каждой стороны от знака равно находится только одно слагаемое. Осталось только разделить слагаемое без x, на коэффициент рядом с неизвестным.
5. Многие уравнения удобно решать графически. Для этого мы все слагаемые собираем с одной стороны уравнения. С другой стороны образуется ноль. Замените его на y, нарисуйте координатные оси и постройте график, имеющейся теперь в наличие функции. Места пересечения графика с осью абсцисс – корни. Запишите.
6. Когда вы выяснили все корни уравнения, не забудьте сличить результаты с найденной ранее областью определения функции. Вне её пределов корней нет, потому как и уравнение не существует.