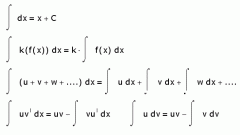Интегральное счисление - основа математического анализа, одного из наиболее непростых дисциплин курса высшей школы. Решать примеры с интегралами требуется как в самом математическом анализе, так и в ряде технических дисциплин. Вся трудность в том, что нет единого алгоритма решения интегралов.
Интегрирование - операция, обратная дифференцированию. Поэтому, для того чтобы хорошо интегрировать, нужно уметь брать производные любых функций. Научиться этому несложно: есть таблица производных, зная которую интегрировать простые функции будет довольно просто.
2
Интегрирование суммы некоторых функций всегда можно представить как сумму интегралов. Пользоваться этим правилам особенно удобно, когда сами функции простые, и их можно вычислить по таблице основных неопределенных интегралов, приведенных ниже.
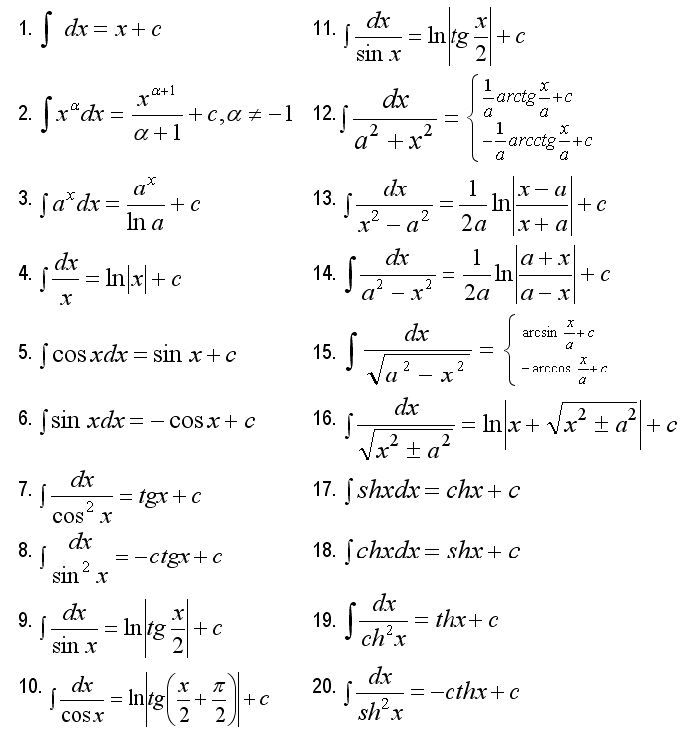
3
Очень важный прием - интегрирование по методу внесения функции под дифференциал. Ей особенно удобно пользоваться тогда, когда внесением под дифференциал - мы берем производную от функции и ставим ее вместо dx (то есть, имеем df(x)'), мы добиваемся того, что функцией под дифференциалом мы пользуемся как переменной.
4
Еще одна базовая формула: Integral(udv)=uv-Integral(vdu) поможет нам в том случае, когда мы сталкиваемся с интегралом от произведения двух элементарных функций. Взять интеграл при ее помощи гораздо проще, чем используя преобразования.
