Инструкция
1
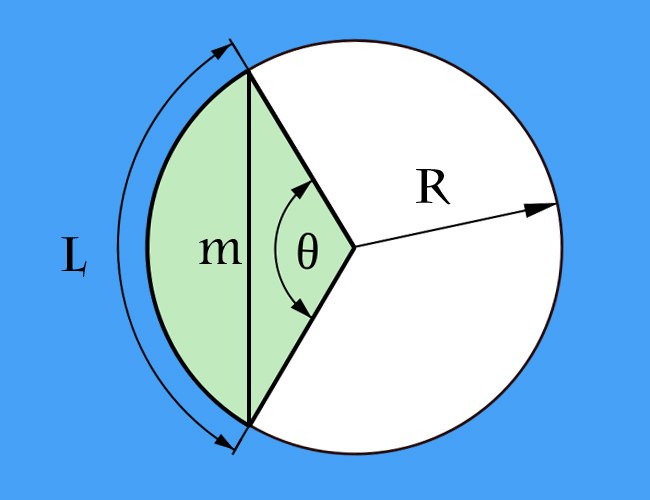
Если длина дуги (l) между крайними точками, задающими хорду, известна, а кроме нее в условиях дан и радиус окружности (R), задачу вычисления длины хорды (m) можно свести к расчету длины основания равнобедренного треугольника. Боковые стороны этого треугольника будут образованы двумя радиусами окружности, а угол между ними будет центральным углом, который вам и нужно рассчитать в первую очередь. Для этого разделите длину дуги на радиус: l/R. Полученный результат выражен в радианах. Если вам удобнее производить вычисления в градусах, формула будет значительно сложнее - сначала умножьте длину дуги на 360, а затем поделите результат на удвоенное произведение числа Пи на радиус: l*360/(2*π*R) = l*180/(π*R).
2
Выяснив величину центрального угла, рассчитайте длину хорды. Для этого удвоенный радиус круга умножьте на синус половины центрального угла. Если вы выбрали расчеты в градусах, в общем виде полученную формулу запишите так: m = 2*R*sin(l*90/(π*R)). Для расчетов в радианах она будет содержать на одно математическое действие меньше m = 2*R*sin(l/(2*R)). Например, при длине дуги в 90 см и радиусе 60 см хорда должна иметь длину 2*60*sin(90*90/(3,14*60)) = 120*sin(8100/188,4) = 120*sin(42,99°) ≈ 120*0,68 = 81,6 см при точности расчетов до двух знаков после запятой.
3
Если в дополнение к длине дуги (l) в условиях задачи дана полная длина окружности (L), выразите через нее радиус, разделив на удвоенное число Пи. Затем подставьте это выражение в общую формулу из предыдущего шага: m = 2*(L/(2*π))*sin(l*90/(π*L/(2*π))). После упрощения выражения у вас должно получиться такое равенство для расчетов в градусах: m = L/π*sin(l*180/L). Для вычислений в радианах оно будет выглядеть так: m = L/π*sin(l*π/L). Например, если длина дуги составляет 90 см, а длина окружности - 376,8 см, длина хорды составит 376,8/3,14*sin(90*180/376,8) = 120*sin(42,99°) ≈ 120*0,68 = 81,6 см.