Вам понадобится
- - радиус окружности:
- - длина дуги хорды;
- - угол дуги хорды;
- - бумага и чертежные инструменты.
Инструкция
1
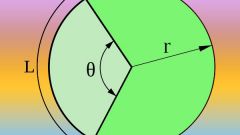
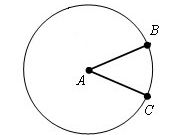
Выполните чертеж в соответствии с условиями задачи. Начертите окружность заданного радиуса. Если вам известен угол дуги, которую стягивает хорда, постройте его. Проведите радиус, отложите с помощью транспортира нужный угол и проведите еще один. Точки пересечения радиусов с окружностью соедините прямой. Это и будет нужная вам хорда. Если же угол неизвестен, начертите произвольную хорду.
2
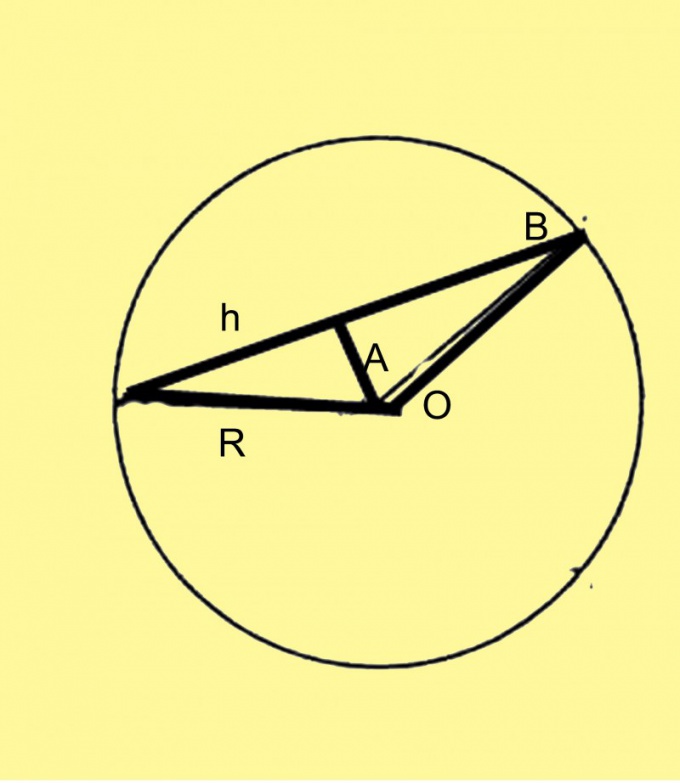
Выполните дополнительное построение. Разделите хорду пополам и проведите к этой точке перпендикуляр из центра окружности. У вас получился равнобедренный треугольник, высотой которого является перпендикуляр к середине хорды.
3
Обозначьте радиус как R, хорду - как h, а центральный угол - как А. Тогда h модно вычислить либо через синус А, либо через косинус. В первом случае формула будет выглядеть как h=2R*sinA/2, где R - известный радиус окружности. Во втором случае формула будет выглядеть как h=R*√(1-cosB).
4
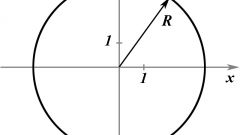
Одна из самых древних геометрических задач - найти длину хорды, если известны радиус окружности и длина дуги. Вычислите длину окружность P. Она равна удвоенному радиусу, умноженному на коэффициент П Выразить ее можно формулой P=2ПR.
5
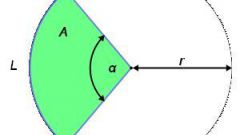
Вычислите отношение заданной длины дуги l к длине окружности P. Таким образом вы вычислите размер угла дуги. В данном случае неважно, будет он в градусах или радианах. Зная его размер, вычислите синус половинного угла. После этого вы можете вычислить размер хорды по уже известной вам формуле.
6
Нередко приходится сталкиваться и с противоположным заданием - например, найти длину дуги по радиусу окружности и длине хорды. Используя теорему синусов, вычислите размер половинного, а затем и целого центрального угла. Зная его, по соотношению длины дуги к длине окружности высчитайте неизвестную вам длину дуги.
Полезный совет
С самой длинной хордой - диаметром - обычно поступают по-другому. Конечно, можно по приведенным соотношениям высчитать и его, но угол известен заранее и составляет 180°. В этом случае sinA/2=sin90°=1. Соответственно, h=2R*sinA/2=2R.
При вычислении размеров любых прямых, так или иначе связанных с окружностью, целесообразно бывает достроить чертеж так, чтобы получились треугольники, параметры которых вам известны. В случае с хордой вы воспользовались несколькими свойствами этой прямой. Например, тем, что перпендикуляр, проведенный к хорде из центра окружности, делит эту хорду пополам.
При вычислении размеров любых прямых, так или иначе связанных с окружностью, целесообразно бывает достроить чертеж так, чтобы получились треугольники, параметры которых вам известны. В случае с хордой вы воспользовались несколькими свойствами этой прямой. Например, тем, что перпендикуляр, проведенный к хорде из центра окружности, делит эту хорду пополам.
Источники:
- как найти длину хорды через радиус