Как вычислить длину дуги

Дугой окружности называется часть окружности, заключенная между двумя ее точками. Ее можно обозначить как AСB, где A и B - ее концы. Длину дуги можно выразить через стягивающую хорду, радиус окружности и угол между радиусами, проведенными к концам хорды.

Инструкция

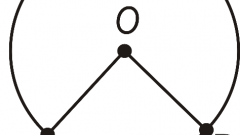
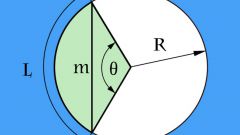
1. Пусть ACB - дуга окружности, R - ее радиус, O - центр окружности. Отрезки OB и OC будут являться радиусами окружности. Пусть угол между ними равен ?. Тогда ACB = R?, где угол ? выражен в радианах, - длина дуги окружности.Если угол ? выражен в градусах, то длина дуги окружности равна: ACB = R*pi*?/180.
2. Хорда AB стягивает дугу AСB. Пусть известна длина хорды AB и угол ? между радиусами OA и OB. Треугольник AOB - равнобедренный, так как OA = OB = R.
3. Высота OE в треугольнике AOB одновременно является его биссектрисой и медианой. Следовательно, угол AOE = AOB/2 = ?/2, а AE = BE = AB/2. Рассмотрите треугольник AEO. Так как OE - высота, то он прямоугольный (угол AOE - прямой). AO - его гипотенуза, а AE - его катет. Отсюда, R = OA = (AB/2)/sin(?/2). Следовательно, ACB = (AB/2)/sin(?/2)*pi*?/180