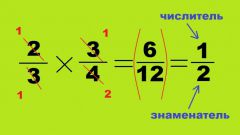Как вычитать дроби

Действия над дробями стали бы полностью аналогичны действиям над целыми числами, если бы не наличие у них знаменателей, зачастую разных. Случаи, когда дроби имеют одинаковые знаменатели, являются наиболее простыми, все прочие случаи в процессе решения необходимо свести к ним. Таким образом, вычитание дробей производится через процедуру приведения их к общему знаменателю.

Инструкция

1. Для начала убедитесь в том, что ваши дроби имею разные знаменатели. В случае, если это не так, вычитание представляет собой вычитание числителей дробей, а знаменатель остаётся прежним. Например, 3/5-1/5=2/5.
2. Чтобы вычитать дроби с разными знаменателями (равно как и для их сложения), требуется сделать их знаменатели одинаковыми.
   Лучшим общим знаменателем является наименьшее общее кратное знаменателей дробей, над которыми производится операция вычитания. Наименьшее общее кратное – это наименьшее натуральное число, которое нацело делится на каждый из знаменателей. Например, наименьшим общим кратным чисел 3 и 5 является число 15.
   Впрочем, в качестве общего знаменателя подойдёт вообще любое общее кратное. Самым простым и верным способом его нахождения является перемножения знаменателей данных дробей.
3. Раз вы меняете знаменатели дробей, нужно изменить и их числители, так, чтобы дроби остались неизменными.
   
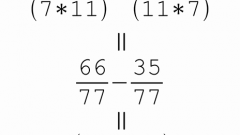
   Домножьте числитель первой дроби на знаменатель второй (и других, если дробей больше, чем две), аналогично поступите с остальными дробями.
4. Теперь вычтите полученные в числителях числа, и припишете общий знаменатель.
5. Лучше всего алгоритм вычитания дробей понятен из примера. Пусть нам нужно рассчитать 5/7-1/2. Общий знаменатель найдём, перемножим знаменатели дробей: 7*2=14. Домножим числитель первой дроби на знаменатель второй: 5*2=10. Затем умножим числитель второй дроби на знаменатель первой: 1*7=7. Теперь вычтем из первого второе: 10-7=3, это и есть числитель итоговой дроби. Припишем общий знаменатель и получим итоговую дробь: 3/14.