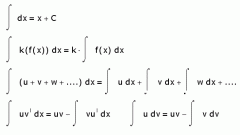Современный математический анализ невозможно себе вообразить без применения понятия интеграла и методов интегрального исчисления. В частности, определенный интеграл прочно закрепился не только в математике, но и в физике, механике и многих других научных дисциплинах. Само понятие интегрирования противоположно дифференцированию и означает объединение частей, например, какой-либо фигуры в целое.
Методы интегрирования уходят корнями в древность. Они были известны еще в Древнем Египте. Есть факты, свидетельствующие о том, что египтянам в 1800 году до нашей эры была известна формула объема усеченной пирамиды. Она и позволила им создать такие шедевры архитектуры, как египетские пирамиды.
Изначально интегралы рассчитывались методом исчерпывания Евдокса. Уже во времена Архимеда с помощью интегрального исчисления усовершенствованным методом Евдокса рассчитывали площади параболы и круга. Современное же понятие определенного интеграла и сам метод ввел Жан Батист Жозеф Фурье примерно в 1820 году.
Без использования математических знаков и формул определенный интеграл можно обозначить, как сумму частей, составляющих геометрическую фигуру, образованную кривой конкретного графика функции. Когда речь идет об определенном интеграле функции f(x), необходимо сразу представить эту самую функцию в системе координат.
Выглядеть такая функция будет в виде кривой линии простирающейся вдоль оси абсцисс, то есть оси иксов, на определенном расстоянии от оси ординат, то есть оси игреков. Когда вы подсчитываете интеграл ∫, вы ограничиваете сначала полученную кривую по оси x. То есть определяете, с какого и по какой момент оси икс вы будете рассматривать данный график функции f(x).
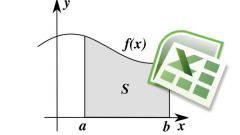
Визуально вы проводите вертикальные линии, соединяющие кривую графика и ось икс в выбранных точках. Таким образом, под кривой образуется геометрическая фигура, напоминающая трапецию. Ее ограничивают проведенные вами линии слева и справа, снизу она обрамляется осью иксов, а сверху – самой кривой графика. Полученная фигура носит наименование криволинейной трапеции.
Для того чтобы подсчитать площадь S такой сложной фигуры, используют определенный интеграл. Именно определенный интеграл функции f(x) на выбранном отрезке по оси иксов позволяет без труда вычислить площадь криволинейной трапеции под кривой графика. В этом и заключается его геометрический смысл.
История определенного интеграла
Методы интегрирования уходят корнями в древность. Они были известны еще в Древнем Египте. Есть факты, свидетельствующие о том, что египтянам в 1800 году до нашей эры была известна формула объема усеченной пирамиды. Она и позволила им создать такие шедевры архитектуры, как египетские пирамиды.
Изначально интегралы рассчитывались методом исчерпывания Евдокса. Уже во времена Архимеда с помощью интегрального исчисления усовершенствованным методом Евдокса рассчитывали площади параболы и круга. Современное же понятие определенного интеграла и сам метод ввел Жан Батист Жозеф Фурье примерно в 1820 году.
Понятие определенного интеграла и его геометрический смысл
Без использования математических знаков и формул определенный интеграл можно обозначить, как сумму частей, составляющих геометрическую фигуру, образованную кривой конкретного графика функции. Когда речь идет об определенном интеграле функции f(x), необходимо сразу представить эту самую функцию в системе координат.
Выглядеть такая функция будет в виде кривой линии простирающейся вдоль оси абсцисс, то есть оси иксов, на определенном расстоянии от оси ординат, то есть оси игреков. Когда вы подсчитываете интеграл ∫, вы ограничиваете сначала полученную кривую по оси x. То есть определяете, с какого и по какой момент оси икс вы будете рассматривать данный график функции f(x).
Визуально вы проводите вертикальные линии, соединяющие кривую графика и ось икс в выбранных точках. Таким образом, под кривой образуется геометрическая фигура, напоминающая трапецию. Ее ограничивают проведенные вами линии слева и справа, снизу она обрамляется осью иксов, а сверху – самой кривой графика. Полученная фигура носит наименование криволинейной трапеции.
Для того чтобы подсчитать площадь S такой сложной фигуры, используют определенный интеграл. Именно определенный интеграл функции f(x) на выбранном отрезке по оси иксов позволяет без труда вычислить площадь криволинейной трапеции под кривой графика. В этом и заключается его геометрический смысл.
Видео по теме