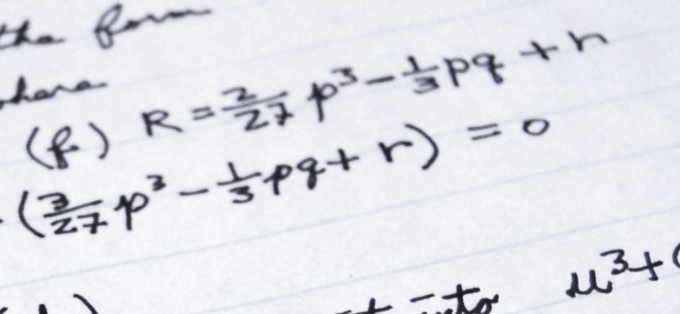Инструкция
1
Задайте функцию в виде формулы, укажите операции и их последовательность выполнения, которые нужно произвести с переменной, чтобы в результате получить значение функции. Этот способ задания функции называется явной формой. Например, ƒ(x)=(x³+1)²−√(x). Область определения этой функции множество [0; +∞). Можно определить функцию таким образом, что при одних значениях аргумента нужно воспользоваться одной формулой, а при других значениях аргумента – другой. Например, функция сигнум x: ƒ(x)=1, если x>0, ƒ(x)=-1 при x<0 и ƒ(0)=0.
2
Составьте уравнение F(x; y)=0 таким образом, чтобы множество его решений (x; y) было таково, что для каждого числа x в этом множестве есть только одна пара (x0; y0) с элементом x0. Такая форма задания функции называется неявной. Например, уравнение x×y+6=0 задает функцию. А уравнение вида x²+y²=1 задает соответствие, но не функцию, так как среди решений этого уравнения есть две пары с совпадающим первым элементом, например, (√(3)/2; 1/2) и (√(3)/2; -1/2).
3
Выразите значения переменных x и y через третью величину, которая называется параметром, то есть задайте функцию в виде x=φ(t), y=ψ(t). Такой вид объявления функции называется параметрическим. Например, x=cos(t), y=sin(t), t∈[-Π/2; Π/2].
4
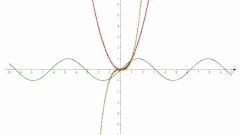
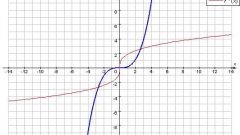
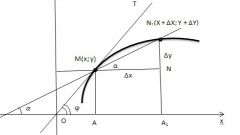
Для наилучшей наглядности задайте функцию в виде графика. Определите систему координат и в ней изобразите множество точек с координатами (x; y). Такой способ объявления функции не позволяет точно определить значения функции, однако очень часто в технике или физике нет возможности задать функцию другим способом.
5
Если множество значений x конечно, то объявите функцию при помощи таблицы. То есть составьте таблицу, в которой каждому значению элемента x ставится в соответствие значение функции ƒ(x).
6
Выразите функциональную зависимость в словесной форме, если нет возможности задать функцию аналитически. Классическим примером является функция Дирихле: «Функция равна 1, если x – рациональное число, функция равно 0, если x – иррациональное число».
Видео по теме