Как вычислить высоту треугольника

Отрезок прямой, проведенный из вершины треугольника в направлении противолежащей стороны и перпендикулярный ей называется высотой треугольника. Противоположная сторона называется основанием, а поскольку вершин и сторон у треугольника по три, то и высот по разным основаниям столько же. В зависимости от известных параметров треугольника, для вычисления высоты можно использовать разные формулы, некоторые из которых приведены ниже.

Инструкция

1. Используйте для нахождения высоты треугольника формулу Ha=2*S/A, если известны его площадь (S) и длина стороны, противолежащей углу, из которого проведена высота (A). Эта сторону называют основанием, а высоту обозначают, как «высота по основанию A» (Ha). Например, если площадь треугольника равна 40 квадратным сантиметрам, а длина основания составляет 10 см, то высота будет вычислена так: 2*40/10 = 8 см.
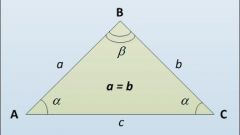
2. Если длина основания не известна, но известна длина прилежащей к нему стороны (B) и угол между основанием и этой стороной (γ), то высоту (Ha) можно выразить, как половину произведения длины этой стороны на синус известного угла: Ha=B*sin(γ). Например, если длина прилегающей стороны равна 10 см, а угол составляет 40°, то высоту можно вычислить так: 10*sin(40°) = 10*0,643 = 6,43 см.
3. Если известны длины всех трех сторон треугольника (A, B и C) и радиус вписанного в него круга (r), то высоту, проведенную из любой из сторон можно выразить как произведение радиуса вписанной окружности на сумму длин сторон треугольника, поделенное на длину основания. Например, для высоты, проведенной из стороны A, эту формулу можно записать так: Ha=r*(A+B+C)/A.
4. Из предыдущей формулы вытекает, что знать длины всех сторон не обязательно, если известны длина периметра (P), длина основания (A) и радиус вписанной в треугольник окружности (r). Тогда для вычисления высоты по основанию A будет достаточно перемножить длину периметра на радиус вписанной окружности и разделить на длину основания: Ha=r*P/A.
5. Если вместо радиуса вписанной окружности известен радиус описанной (R) и длины всех сторон треугольника (A, B и C), то для нахождения высоты по любому основанию надо перемножить длины всех сторон, а полученный результат разделить на удвоенное произведение радиуса описанной окружности на длину основания. Например, для высоты, проведенной из стороны A, эту формулу можно записать так: Ha=A*B*C/(2*R*A).