Вам понадобится
  • чистый лист бумаги;
  • карандаш;
  • линейка;
  • учебник по геометрии.
Инструкция
1
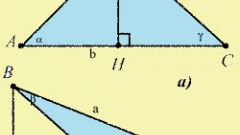
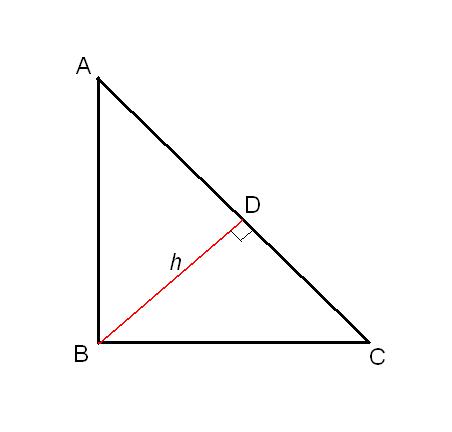
Рассмотрим прямоугольный треугольник ABC, где ∠ABC = 90°. Опустим из этого угла высоту h на гипотенузу AC, точку пересечения высоты с гипотенузой обозначим D.
Как найти высоту в прямоугольном треугольнике
2
Треугольник ADB подобен треугольнику ABC по двум углам: ∠ABC = ∠ADB = 90°, ∠BAD - общий. Из подобия треугольников получаем соотношение сторон: AD/AB = BD/BC = AB/AC. Берем первое и последнее соотношение пропорции и получаем, что AD = AB²/AC.
3
Поскольку треугольник ADB прямоугольный, для него справедлива теорема Пифагора: AB² = AD² + BD². Подставляем в это равенство AD. Получается, что BD² = AB² - (AB²/AC)². Или, что то же, BD² = AB²(AC²-AB²)/AC². Так как треугольник ABC прямоугольный, то AC² - AB² = BC², тогда получим BD² = AB²BC²/AC² или, извлекая корень из обеих частей равенства, BD = AB*BC/AC.
4
С другой стороны, треугольник BDC также подобен треугольнику ABC по двум углам: ∠ABC = ∠BDC = 90°, ∠DCB - общий. Из подобия этих треугольников получаем соотношение сторон: BD/AB = DC/BC = BC/AC. Из этой пропорции выражаем DC через стороны изначального прямоугольного треугольника. Для этого рассматриваем второе равенство в пропорции и получаем, что DC = BC²/AC.
5
Из соотношения, полученного в шаге 2, имеем, что AB² = AD*AC. Из шага 4 имеем, что BC² = DC*AC. Тогда BD² = (AB*BC/AC)² = AD*AC*DC*AC/AC² = AD*DC. Таким образом, высота BD равна корню из произведения AD и DC или, как говорят, среднему геометрическому частей, на которые эта высота разбивает гипотенузу треугольника.